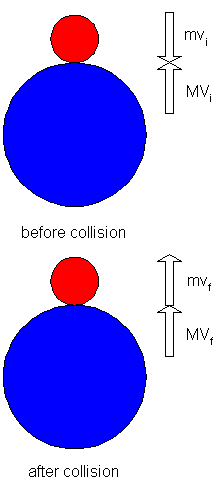
 After the collision, the momentum is pf = mvf + MVf, and the kinetic energy is KEf = (1/2)mvf2 + (1/2)MVf2.
So we have two equations:
After the collision, the momentum is pf = mvf + MVf, and the kinetic energy is KEf = (1/2)mvf2 + (1/2)MVf2.
So we have two equations:
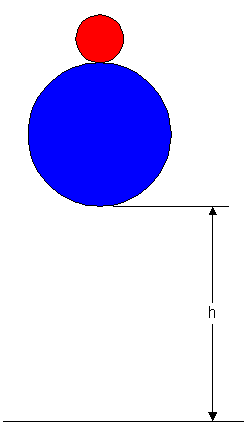
A classic demonstration of collisions and conservation of momentum involves dropping a large ball, a basketball for instance, with a small ball sitting on top, a baseball or superball, as pictured at right. When the large ball hits the floor the small ball is propelled to a considerable height, much higher than where it was dropped from.
To analyse this situation, we must think in terms of a collision. Not a collision between the large ball and the floor, but a collision between the large ball bouncing upward from the floor, and the small ball still moving downward. To determine how high the small ball will bounce, I will make the following assumptions and approximations:
First, I need to determine the speed of each ball before their collision. Since the large ball falls a distance h to the floor, its kinetic energy is (1/2)MVi2 = Mgh, so its speed is Vi = Sqrt{2gh}. Since it bounces elastically from the floor, this will be its upward speed. The small ball also falls a distance h, so its speed just before the collision is also vi = Sqrt{2gh}. Therefore the initial momentum of the pair is pi = (M-m)Sqrt{2gh} upward, and the initial kinetic energy is KEi = (1/2)(M+m)(2gh) = (M+m)gh.
 After the collision, the momentum is pf = mvf + MVf, and the kinetic energy is KEf = (1/2)mvf2 + (1/2)MVf2.
So we have two equations:
After the collision, the momentum is pf = mvf + MVf, and the kinetic energy is KEf = (1/2)mvf2 + (1/2)MVf2.
So we have two equations:
To solve for vf, use the first equation to get Vf and substitute into the second.
Now I'll make use of the fact that m«M, such that (1+m/M)=1, (M-m)=M, and (M-m)²/M=M-2m.
Then
mvf² - 2Sqrt{2gh}mvf - 6mgh = 0
This quadratic equation has the solution (note that m factors out):
vf = -Sqrt{2gh} or 3Sqrt{2gh}.
The first number is the speed before the collision, not the answer we are looking for.
The second answer is the one we want.
This says that the small ball rebounds with 3 times the velocity it began with.
With 3 times the velocity, the small ball will rise to a height 9 times greater than where it started.
You can show this by using conservation of energy.
This calculation assumed that the collisions are elastic. In my demonstration, this was clearly not true, since, when dropped to the floor, neither ball would bounce back to the height it was dropped from. But since they did bounce, the collisions were not completely inelastic. The true situation lies somewhere in between, and the result is that the small ball rebounds higher than where is was dropped from, but not 9 times higher.