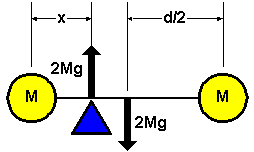
For instance, consider the barbell from the previous lecture.
I calculated the gravitational force for each weight separately, and used the two forces to determine the torque.
But, there is another approach.
The first condition for equilibrium, from Chapter 4, is that the net force acting on an object must be zero.
In fact, we can write this down for the x and y components separately:
SFx =0, and SFy =0
Now consider the barbell example given above.
All the applied forces, gravity and the normal force from the support, act in the y direction, and they sum to zero.
Yet, unless the support is exactly in the middle of the barbell, there will be a net torque, and the barbell will tend to rotate.
We cannot say it is in equilibrium!
But this does lead to a second condition for equilibrium, mainly that the net torque must also be zero.
To the above force equations we should add:
St = 0.
The primary implication is that not only must we pay attention to the size and direction of the applied forces, but also their point of application on an object.
The chewing muscle, the masseter, is one of the strongest in the human body. It is attached to the mandible (lower jawbone), as shown in Figure P8.13a. The jawbone is pivoted about a socket just in front of the auditory canal. The forces acting on the jawbone are equivalent to those acting on the curved bar in Figure P8.13b: C is the force exerted against the jawbone by the food being chewed, T is the tension in the masseter, and R is the force exerted on the mandible by the socket. Find T and R if you bite down on a piece of steak with a force of 50.0N.
We must apply the two conditions for equilibrium (this of course assumes that the jaw doesn't move):
T - C - R = 0, and
C(11 cm) - T(3.5 cm) + R(0 cm) = 0.
From the second equation, we find T = C(11 cm)/(3.5 cm) = (50.0N)(11cm)/(3.5cm) = 157 N.
Then from the first equation we find that R = T - C = 157N - 50.0N = 107N.
| If the object is in equilibrium, it doesn't matter where you put the axis of rotation for calculating the net torque; the location of the axis is completely arbitrary. |
How do we handle the force of gravity for an extended object? Up to now we've simply taken gravity as acting on an object, with no real concern for where it acts. But now, to handle torques, we must concern outselves with where the force of gravity acts on an object.
For instance, consider the barbell from the previous lecture.
I calculated the gravitational force for each weight separately, and used the two forces to determine the torque.
But, there is another approach.
What if we take the total mass of the barbell, 2M, and say that the gravitational force due to the total mass acts at the center of the barbell. Then the torque is t = 2Mg(x-d/2) = Mg(2x-d), the same result arrived at previously. We call the point at the center of the barbell its center of gravity. We can consider the net gravitational force as acting on (or at) the center of gravity.
We define center of gravity (a.k.a. center of mass) of an object as the point (not necessarily on the object) through which the total gravitational force acts, regardless of the orientation of the object.
The barbell is a rather symmetric object, and finding its center of gravity is easy. The center of gravity of a homogeneous, symmetric object lies on the "axis of symmetry". Notice that we already implicitly assumed that the force of gravity acted at the center of the spherical weights of the barbell.
For an object without symmetry, we need a mathematical expression:
xcg = (m1x1 + m2x2 + m3x3 + ...)/(m1 + m2 + m3 + ...) = Smixi/Smi
To apply the above expression, break the object up into n symmetrical or point objects, each with mass mi and c.g. located at xi.
Then the calculation will yield the x coordinate of the center of gravity of the composite object.
To determine the y coordinate of the center of gravity, apply the same technique, exchanging y for x in the expression.
A water molecule consists of an oxygen atom with two hydrogen atoms bound to it. The bonds are 0.100 nm in length and the angle between the two bonds is 106°. Determine the location of the center of gravity of the molecule. Consider the mass of an oxygen atom to be 16 times the mass of a hydrogen atom. See the figure in the text.
There is symmetry about the x-axis. If we flip the water molecule around the x-axis, we get back the same water molecule (all H atoms are identical and indistinguishable). Therefore, the c.g. must lie on the x-axis, giving ycg = 0.
We can find xcg using the equation given above. Let's call the center of the oxygen atom x=0. Then xcg = ((0)(16mH) + 2(0.100 nm)cos53° mH)/(16mH + 2mH) = 0.00669 nm from the oxygen atom.
So the center of mass of the water molecule is located at (xcg, ycg) = (0.00669, 0) nm.
Why does holding a long pole help a tightrope walker stay balanced?
With a long pole, the tightrope walker can lower his center of gravity. (If the pole is curved, he can even get his center of gravity below the rope.) A lower center of gravity means that the torque exerted on him, due to misalignment of the cg with the rope, is reduced.
When a car speeds up, the front rises, and when it brakes, the front drops. Why?
The force that accelerates or decelerates a car comes ultimately from the contact of the tires with the road. The body of a car is attached to the wheels through a "suspension" which allows for independent motion to help smooth over bumps. The suspension serves as an axis of rotation, and because it is located above the road surface, there is a lever arm. The force applied to speed up a car will produce a torque which tends to rotate the front of the car upward, and a braking force produces a torque which tends to rotate the front downward.
A 500 N uniform rectangular sign 4.00 m wide and 3.00 m high is suspended from a horizontal, 6.00 m long, uniform, 100 N rod, as drawn. The left end of the rod is supported by a hinge and the right end is supported is supported by a thin cable making a 30.0° angle with the vertical. (a) Find the tension, T, in the cable. (b) Find the horizontal and vertical components of force exerted on the left end of the rod by the hinge (or wall).
We can determine the tension in the cable by determining the force required on the end of the rod to keep it in equilibrium; the tension is this force. Begin by drawing a force diagram for the rod. First, consider the rod and sign as one object. Their combined center of gravity is at xcg = [(3.00 m)(100 N) + (4.00 m)(500 N)]/(100 N + 500 N) = 3.83 m. Therefore, the weight of the rod and sign, 600 N, acts at a point 3.83 m from the wall. In addition to the weight, there is the force from the tension in the cable, which acts in the direction of the cable, and the force of the hinge, which acts in an indetermined direction. For convenience, let's call the x and y components of the hinge force Fx and Fy.
Next, apply the first condition for equilibrium, that the x and y components of the forces on the rod must sum to zero.
For the x direction, we get:
T sin30° = Fx
And for the y direction:
T cos30° + Fy = 600 N
Finally, apply the second condition for equilibrium, that the sum of the torques is zero.
As long as the rod is stationary, we can calculate the torque about any convenient axis.
The usual approach is to pick one of the three locations where forces are applied, as this will remove one of the forces from the torque calculation (the lever arm will be zero).
I will choose the axis of rotation at the hinge, and the resulting torque equation is:
(6.00 m)T cos30° - (3.83 m)(600 N) = 0
(a) From this last equation we find T = (3.83 m)(600 N)/(6.00 m)cos30° = 442 N.
(b) Use this result with the first 2 equilibrium equations to find the x and y components of the hinge force.
Fx = T sin30° = (442 N)sin30° = 221 N, and
Fy = 600 N - T cos30° = 600 N - (442 N)cos30° = 217 N.
Y will be obtain the same result if you work the problem with a different axis of rotation. Try it and see.
A 15.0 m, 500 N uniform ladder rests against a frictionless wall, making an angle of 60.0° with the horizontal, as shown. (a) Find the horizontal and vertical forces exerted on the base of the ladder by the Earth when an 800 N fire fighter is 4.00 m from the bottom. (b) If the ladder is just on the verge of slipping when the fire fighter is 9.00 m up, what is the coefficient of static friction between ladder and ground?
Again, start by drawing a force diagram for the ladder, being careful to note the location where forces are applied.
Since the ladder is uniform, its center of gravity is right in the middle, 7.5 m from either end.
The first condition for equilibrium gives:
nwall - Fx = 0
Fy - 500 N - 800 N = 0 or Fy = 1300 N
Since the wall is frictionless, there is no vertical force from the wall.
The second condition for equilibrium, choosing the base of the ladder as the axis of rotation, gives:
(500 N)(7.50 m)cos60° + (800 N)(4.00m)cos60° - nwall(15.0 m)sin60° = 0
The last equation gives
nwall = [(500 N)(7.50 m)cos60° + (800 N)(4.00m)cos60°]/(15.0 m) sin60° = 268 N
Thus Fx = nwall = 268 N, and Fy = 1300 N for part (a).
(b) To determine the coefficient of static friction, we need the x component of the force on the base of the ladder, equal to the friction force, and the y component, equal to the normal force.
The coefficient of friction is the ratio Fx/Fy.
When the fire fighter is 9.00 m up the ladder, the equilibrium equations read:
nwall - Fx = 0
Fy - 500 N - 800 N = 0 or Fy = 1300 N
(500 N)(7.50 m)cos60° + (800 N)(9.00m)cos60° - nwall(15.0 m)sin60° = 0
We find that Fx = nwall = 421 N, and again Fy = 1300 N.
This give ms = Fx/Fy = 421 N/1300 N = 0.324.
Consider a mass, m, fixed to a central point by a string of length r, and moving about that point in a circle on a frictionless surface. If a tangential force is applied to the mass, it will experience a tangential acceleration given by Ft = mat. Multiply both sides of this expression by the radius, so that the left hand side is the torque, to get Ftr = t = mrat. Now use the relation at = ra and the expression becomes t = mr2a. This relation says that the torque is proportional to (or produces) the angular acceleration, times a factor of mr2. The factor mr2 is called the moment of inertia.
What if the rotating object is not a small mass at the end of a string, but a larger object, like a wheel, a cylinder, or a sphere?
In this case, consider the extended object as being composed of lots of little pieces, each piece feeling a torque.
Then the total torque is the sum of the torques on each piece:
ttot = St = S(mr2a).
Since the angular acceleration, a, is the same for all the pieces of the object, it can be factored out of the sum in the last expression to yield:
ttot = (Smr2) a.
We call I = Smr2 the moment of inertia of the object, and then write ttot = Ia, the rotational analog of F = ma.