course index

Ch. 27: Quantum Physics

The theories of special and general relativity represent on of two major developments in Physics in the early 20_th century. The second major development is quantum theory.

While special relativity is important for the study objects that move at close to the speed of light, and general relativity is important for the study of very massive objects, quantum theory is important for the study of very small objects (molecules, atoms, nuclei, and particles) or processes where small amounts of energy are transferred (transistors, superconductors, and blackbody radiation).

Recall that the expressions of special relativity reduce to the traditional expressions in the case of small velocities. This was required so that the results of "classical" or "Newtonian" Physics are reproduced. The same reduction holds for quantum Physics -- results from quantum theory must reduce to the "classical" Physics results as the objects involved become large (more massive) or the energy exchanged becomes large.

27.1 Blackbody Radiation and Planck's Hypothesis

We traditionally begin discussing quantum Physics with the rather mundane sounding topic of blackbody radiation. Historically this topic marks the introduction of quantized energy, the basis of quantum theory.

A blackbody is something that absorbs all the light incident on it. The concept of a blackbody is introduced in section 11.7 of the text, in a discussion of heat transfer by radiation. The basic idea is that a blackbody at temperature T emits heat in the form of radiation according to Stefan's law:

With the understanding that light is electromagnetic radiation, physicists began investigating the properties of blackbody radiation. For experimenters, a blackbody is constructed by a hollow cavity with a small hole from which the radiation can emerge. I tend to think of this like a hot oven as used in glass blowing. It was discovered that the radiation is emitted with a particular spectrum which only depends on the temperature of the blackbody. That is, the different wavelengths of infrared, visible, and ultraviolet radiation come in proportions that only depend on the temperature. (drawing of spectrum) The peak of the spectrum is given by Wien's displacement law:

Attempts to explain the spectrum using classical physics failed. They always tended to predict too much radiation with small wavelengths, hence known by the term "ultraviolet catastrophe".

Max Planck came up with a solution to the problem that involved two assumptions:

1. The radiation inside the blackbody is absorbed and re-emitted from the walls. The wall is composed of "resonators" which can have only certain discrete energy values, E_n = nhf, where n is a positive integer called the "quantum number", f is the frequency of the resonator, and h is Planck's constant:
   h = 6.626×10^-34J s
   We say that the energy of the resonators is "quantized".
2. The second assumption is that the electromagnetic radiation is also quantized, it comes in packets called photons. When radiation is absorbed or emitted, the resonator changes from one quantum state to another; if the resonater does not change state, no energy is emitted or absorbed. If the resonater changes from the state with n=3 to the state with n=2, then a photon is emitted with energy
   E = 3hf - 2hf = hf.

With the addition of these assumptions, Planck was able to explain the observed blackbody spectrum exactly.

In recent years, the importance of this mundane topic has grown and flourished. The reason is that space, the universe, acts like a blackbody (at least in regions away from the sun, planets, stars and galaxies). The blackbody radiation of the universe was discovered in the 1940's when some Bell Labs researchers were trying to set up a microwave receiver. Their receiver was picking up noise that was soon realized to be radiation from the "cosmic microwave background" (CMB).

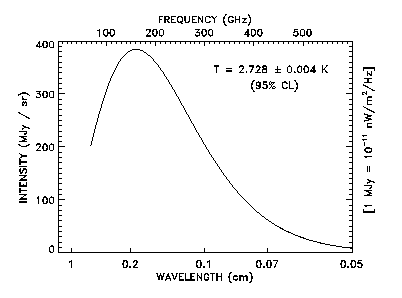
The cosmic microwave background is a remnant of the "big bang". It has more recently been measured with incredible accuracy by experiments such as the COBE satellite. Their result is pictured below. The shape of this spectrum is exactly as predicted for a black body of temperature T = 2.782°K.