PHY5200 F06
Chapter 3: Momentum and Angular Momentum
Reading
Taylor 3.1-3.3 (today) and Monday we will review for the Midterm
Recall
Conservation of Momentum: P[dot] = Fext.
Applied to a rocket, this yields v = v0 + vexln(m0/m).
Systems of Particles
Up to now we've applied Newton's laws to "point-like" particles only. Even when speaking of objects that are clearly not point-like, such as blocks, cars, trucks, and pendulum bobs, we've somehow managed to ignore the physical extent of the object. Although not yet shown, this treatment is justified to the extent that the body is rigid and not rotating (spinning or twisting). Now we will begin to investigate the case of "rigid" bodies, objects with a fixed, rigid, physical size. To understand how Newton's laws apply in this case, we start with a system of point-like particles, each particle obeying Newton's laws in the ways we have already studied. By summing the effects of all the particles, we will obtain results we will then apply to rigid bodies
The result for a system of particles is that the motion can be decomposed into three parts:
- The motion of the center of mass (CM) of the entire system governed by forces external to the system.
- Rotation about the CM governed by external torques.
- Internal motion governed by interactions between particles in the system.
The Center of Mass
For a system of n particles, we define the center of mass (CM) of the system as
rCM = (m1r1 + m2r2 + ... + mnrn) / (m1 + m2 + ... + mn) = (1/M) ∑i mi ri
where mi and ri are the mass and position vector of the ith particle, and M = ∑i mi is the total mass of the system. The velocity of the center of mass is found by differentiating with respect to time:
vCM = drCM / dt = (1/M) ∑i mi dri / dt = (1/M) ∑i mi vi
Logically we define the center of mass momentum as the total mass times of the system times the center of mass velocity. The result is:
pCM = M vCM = ∑i mi vi = ∑i pi
To summarize, the momentum of the center of mass of a system of particles is equal to the vector sum of the momenta of the particles.
Forces: Internal and External
Suppose each particle is acted on by an external force Fi, and particle j exerts a force Fij on particle i.
By Newton's third law, particle i exerts a force on particle j that is equal in magnitude and opposite in direction, Fij = -Fji.
The total force acting on particle i is
Ftoti = Fi + ∑j Fij
where we include a term Fii in the sum for convenience, but we force this term to be zero. The total force acting on the system is the sum of the forces acting on each part of the system.
Ftot = ∑i Ftot i = ∑i Fi + ∑i≠j Fji = ∑i Fi = ∑i dpi / dt = dpCM / dt
This statement says that we can treat the overall motion of a system of particles as if we had a single particle of mass M located at the center of mass of the system, and subject to the total external force on the system.
This is an enormous simplification!
No matter how the system of particles is arranged, or how complex is their internal interactions, we can treat the entire system as a single particle located at the center of mass of the system for the purposes of understanding the overall motion -- that is, the motion of the center of mass.
Example:
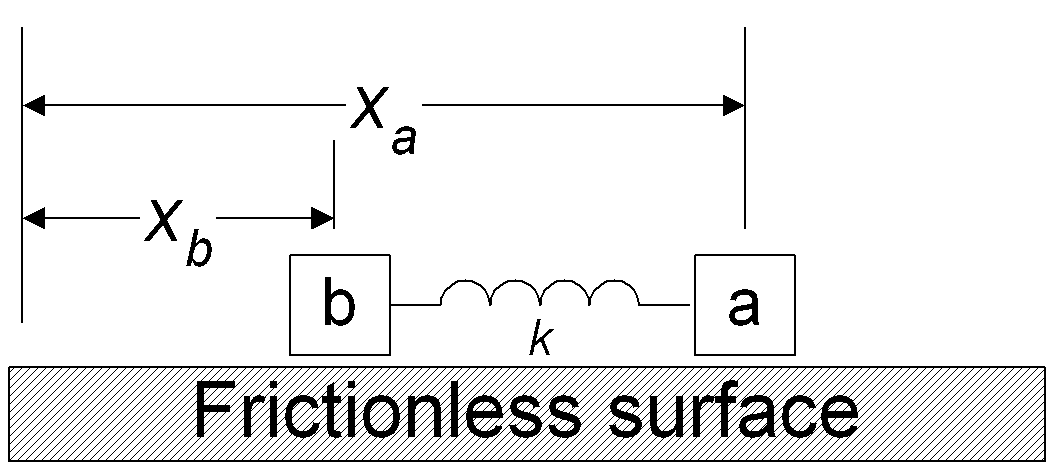
Two identical blocks, a and b, slide on a frictionless track.
Each has mass m and they are attached by a massless spring of length l and spring constant k.
Initially they are at rest.
At t=0 block a is hit sharply giving it an instantaneous velocity v0 away from b.
Determine the motion of the blocks for all later times.
Let's begin by finding the motion of the center of mass.
Calling the positions of a and b, xa and xb , the location of the center of mass is given by
xCM = (maxa + mbxb)/(ma + mb) = (xa + xb)/2
The position of the center of mass is halfway between the two masses, right where one would guess it should be.
Angular Momentum for a Single Particle
For a single particle, angular momentum is defined as L = r × p.
Angular momentum is a vector quantity, but has the odd property that it is perpendicular to the plane of motion -- the plane containing r and p.
Perhaps you recall from introductory physics that the time rate of change of L is equal to the applied torque, N = r × F. We can derive this by evaluating the time derivative of L.
dL/dt = d/dt (r × p) = (dr/dt)× p + r ×(dp/dt) = r ×(dp/dt) = r × F = N
The first cross product is zero because the velocity is parallel to the momentum, v × p = m(v × v) = 0.
An angular momentum usually (but not always) means that we are dealing with some sort of rotation, like a spinning wheel, or planets orbiting a sun.
A rotation has a center where it is natural to place the origin of coordinates, but up to now we haven't made use of this fact.
We will now, in connection with the idea of central forces.
A central force is one that points along the line connecting two interacting objects.
The gravitational and electrostatic forces are central forces.
Friction and the Lorentz magnetic force are not.
If a situation involves a central force, and we measure position from the center of force, then r and F are parallel and the torque N is zero, and the angular momentum L is constant.
This is the law of conservation of angular momentum: if the applied torque is zero then angular momentum is conserved.
Kepler's Second Law
Angular Momentum for Several Particles
The moment of inertia
We would like to derive a similar result for a system of particles.
For a system of particles, we define the total angular momentum as the vector sum of the individual particle angular momenta, Ltot = ∑i Li = ∑i ri × pi.
Let's look at the time derivative of this angular momentum.
d Ltot / dt = ∑i [ ( d ri / dt ) × pi ] + ∑i [ ri × ( d pi / dt ) ] = ∑i [ ri × (d pi / dt ) ]
As above, we'll use Newton's second law to substitute the force on particle i for the momentum derivative term. When considering a single particle, all forces are external. This time though, we have internal and external forces. From the previous lecture we have:
d pi / dt = Ftoti = Fi + ∑j Fij
Inserting this expression in the one above gives:
dLtot/dt = ∑i
ri × Fi + ∑i∑j ri × Fij = ∑i ri × Fi = Ntot
the result we wanted.
The double sum of the internal forces is zero assuming that the forces between particles are central.
Here's the explanation.
Due to Newton's third law, for every force Fij its pair Fji = -Fij.
Combining these two terms yields
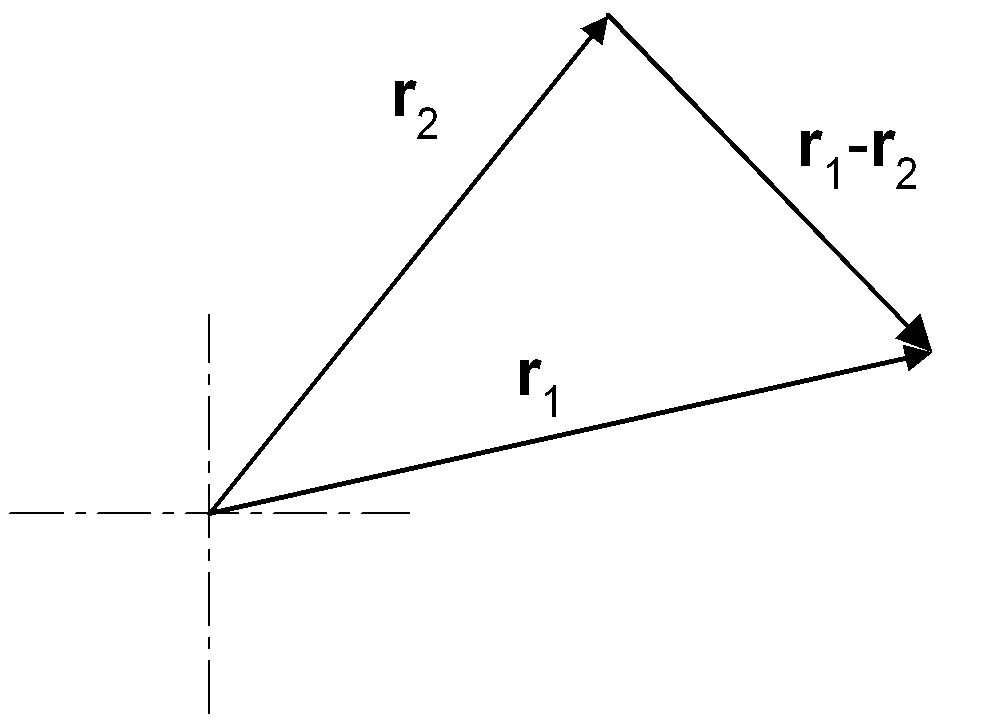
ri × Fji + rj × Fij = ri × Fij - rj × Fji = (ri - rj) × Fij = 0
The quantity ri - rj is a vector pointing from particle i to particle j.
If Fij is a central force, then it also points along the line from particle i to particle j; therefore the vectors in the cross product are parallel, and the cross product is zero.
Angular momentum about the CM
Since we will often deal with the CM, it is useful to express the angular momentum in terms of the CM of the system.
Recall how we used CM coordinates in the example from last lecture.
Let's do that again here, r'i = ri - rCM, and likewise we can express the velocity in terms of the CM velocity and the part relative to the CM.
Ltot = ∑i (rCM + r'i) × mi (vCM + v'i) =
rCM × pCM + rCM × ∑i mi v'i + ∑i mi r'i × vCM + ∑i mi r'i × v'i =
rCM × pCM + ∑i r'i × p'i
To reach this solution I've used ∑i mi v'i = 0 and ∑i mir'i = 0.
Can you see why these are true?
Hint, try calculating rCM by expressing the coordinates in terms of the CM coordinates and the coordinate of the CM.
The above result says that the total angular momentum of a system of particles is composed of two parts: the angular momentum of the CM and the angular momentum about the CM. The second part is what we normally think of as the rotation or spinning of something.
The first part we might consider as the angular momentum due to the orbit, or path of our system.
This is quite a convenient occurance; the center of mass is a special point indeed.
Let's summarize.
The motion of the center of mass is governed by the external forces acting on the system. Internal forces contribute to internal motion, but don't affect the motion of the CM.
The time rate of change of the total angular momentum of a system equals the net external torque.
The total angular momentum is composed of two components, the angular momentum due to rotations about the center of mass, and the angular momentum of the orbit of the center of mass.
The overall idea when analyzing the motion of a system is to take a top down approach. Start with the motion of the CM of the system.
Then look for rotations about the center of mass (a collective motion).
Finally, consider the individual motions of particles relative to the CM.
Kinetic Energy
For a system of n particles the kinetic energy is the sum of the individual kinetic energies:
Ttot = ∑i Ti = ∑i ½mivi²
Now if we express vi in terms of the CM velocities, we can break the kinetic energy into a piece due to the motion of the CM and a piece due to the relative motions of the particles.
vi² = (vCM + v'i)⋅(vCM + v'i) = vCM² + v'i² + 2vCM⋅v'i
Inserting this into the kinetic energy expression, and noting that the remaining dot product sums to zero, we get:
Ttot = ½MvCM² + ∑i ½miv'i² = TCM + Trel
In words, the total kinetic energy of a system is equal to the kinetic energy due to the motion of the CM plus the kinetic energy due to motion of particles of the system relative to their CM.
This latter part can come from rotation of the system (a collective motion of all the particles of the system), or the motion of individual particles of the system.
Example: Kinetic Energy of the Swinging Rod
Calculate the kinetic energies of CM motion and relative motion for a swinging rod.
TCM = ½mvCM² = (1/8)m2lω²
Trel = ∑i ½miv'i² = ½ω² ∑i mir'i² --> ½ω² ∫ r²dm = 2½ω² ∫0l/2 r²dm = (1/24) mω²l²
Ttot = ½ω² ∫0l r²dm = (1/6)mω²l²
A quick check confirms that Ttot = TCM + Trel.
Collisions
Collisions are an important tool in physics. Much of our understanding of the subatomic world comes from the study of collisions between subatomic particles. Many aspects of the motion of comets and man-made satellites can be understood as "collisions" with planets and stars. And even the physics of semiconductors and superconductors is phrased in the language of collisions.
In a collision, two objects approach each other, interact, and then continue with their motion. We generally assume that their interaction occurs over a finite time and distance, then, even without knowing the details of their interaction (gravitational, electrical, or any other 'al) we can understand the kinematics of the collision. The reason is conservation of momentum and energy.
- In the usual situation, there are no external forces on the two objects. Therefore, the total momentum of the two objects is conserved. This is always true independent of whether the forces between the objects are conservative or not.
- Total energy is conserved in the collision, but sometimes the collision process transforms some of the energy from mechanical to other forms, for instance heat. We quantify the degree of energy conservation by the quantity e
= D
v'/D
v. If e
=1, mechanical energy is conserved, and we say that the collision is elastic. For e
¹
1, mechanical energy is not conserved, and we say that the collision is inelastic.
Example: Double Ball Drop
Impulse
© Robert Harr 2006

