PHY5200 F07

Chapter 2: Projectiles and Particles

Reading

Taylor 2.4-2.6 (today) and 2.7-3.1 (Wednesday)

Recall

Vertical motion with quadratic drag

For one-dimensional motion subject to both gravity and quadratic drag, the equation of motion is

m(dv/dt) = mg - cv²

where I've chose gravity in the positive direction (y axis pointing downward). When the drag force equals the weight, the net force on the object is zero and it ceases to accelerate or decelerate. This occurs at the terminal velocity

v_ter = (mg/c)^½.

This is the speed that a falling object will eventually obtain, independent of its initial velocity.

Using the terminal velocity, we can rewrite the equation of motion as

d_tv = g(1 - [v²/v_ter²])

and use the technique of separation of variables to obtain

dv / (1-v²/v_ter²) = gdt .

Let's specialize to the case of an object starting from rest, and integrate this expression from 0 to t in t, and from 0 to v in v:

(v_ter/g) arctanh(v/v_ter) = t

or, solving for v as a function of t

v(t) = v_ter tanh(gt/v_ter)

where tanh is the hyperbolic tangent function

tanh(z) = (e^z - e^-z) / (e^z + e^-z)

and arctanh is the inverse hyperbolic tangent function.

The hyperbolic functions

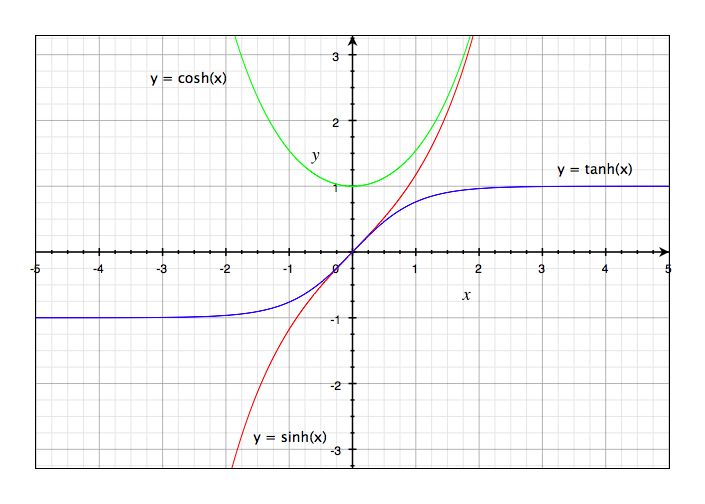
The hyperbolic functions are a set of functions connected to the standard trigonometric fucntions: sin, cos, tan, and their inverses. The hyperbolic sine (sinh), cosine (cosh), and tangent (tanh) functions are graphed above. The hyperbolic tangent appears in a number of situations. It has the properties of tanh(0)=0, d(tanh(z))/dz=1 for z=1, tanh(∞)=+1, tanh(-∞)=-1. The hyperbolic sine and cosine functions are defined as

sinh(z) = ½(e^z - e^-z) cosh(z) = ½(e^z + e^-z)

They have the following properties: sinh(0) = 0, d(sinh(z))/dz = 1 for z=0, sinh(∞) = ∞, sinh(-∞) = -∞, cosh(0) = 1, d(cosh(z)/dz = 0 for z=0, cosh(∞) = cosh(-∞) = ∞. The hyperbolic tangent has the same relation to the hyperbolic sine and cosine functions as tangent has with sine and cosine, that is,

tanh(z) = sinh(z)/cosh(z) = (e^z - e^-z) / (e^z + e^-z).

Position as a function of time

Now back to the discussion of vertical motion with quadratic drag. Integrate to find the postion as a function of time

y(t) = (v_ter²/g) ln[cosh(gt/v_ter)]

Note that for large values of time, we can simplify this expression since the cosh function is approximately ½e^gt/v_ter (neglecting the negative exponential term) and upon taking the log we have

y(t) ≈ (v_ter²/g) (ln½ + gt/v_ter) ≈ v_tert - 0.693(v_ter²/g)

We see that the position approaches what we would have for motion with a constant velocity v_ter, differing from it by the final term.

Quadratic drag with horizontal and vertical motion

The equation of motion for a projectile subject to forces of gravity and quadratic drag, moving in two dimensions, is:

m d_tv = mg - c(v_x²+v_y²)^½v

Resoloving this expressions into components yields two coupled first order differential equations:

m d_tv_x = -c(v_x²+v_y²)^½v_x

m d_tv_y = -mg - c(v_x²+v_y²)^½v_y

These cannot be solved in closed form, outside of some special cases, such as when the motion is limited to one dimension, as treated earlier. In general, these must be solved numerically.

Please see read the example of the numerical solution for the motion of a baseball discussed in the text (Example 2.5). Some, hopefully, obvious features are seen. The object's maximum height and range are smaller than in the solution without air resistance. The object reaches it's maximum height sooner then in the vacuum solution. And, maybe not so obviously, there is a maximum distance which the object will move in the horizontal direction, no matter how far it drops vertically (there is a vertical asymptote to the motion). The appearance of a limit to the x motion is surprising, since there was no limit in the case of one-dimensional horizontal motion with quadratic drag.

To see how the limit arises, consider again the equations of motion. If the object has fallen substantially in the vertical direction, then the y velocity will approach the terminal velocity.

Motion of a Charge in a Uniform Magnetic Field

A charged particle moving through a magnetic field is subject to the Lorentz force

F = qv×B

where q is the particle's charge, v is the particle's velocity at a location r, and B is the magnetic field at location r. The magnetic field can change with position, but we will consider the relatively simple case when the magnetic field is constant, and choose the z axis of our coordinate system to be parallel to the magnetic field, B = Bzhat. This is an odd force, first because it is velocity dependent, and second because it is perpendicular to the direction of motion. But you are probably already familiar with the result for the motion of a charged particle in a uniform magnetic field. We'll look at how this problem is solved using techniques you've learned, with one additional twist.

The equation of motion for a charged particle moving in a uniform magnetic field is

mv[dot] = qv×B

The component equations are (assuming B points in the +z direction)

mv_x[dot] = qBv_y

mv_y[dot] = -qBv_x

mv_z[dot] = 0

From the last equation we have v_z = v_z0 = constant. The x and y component equations are linear, coupled differential equaitons. The solution of these is an opportunity to demonstrate the method of change of variables.

Define ω = qB/m. The quantity ω is known as the cyclotron frequency, for reasons that are explained a little later. We can rewrite the x and y equations with ω as

v_x[dot] = ωv_y

v_y[dot] = -ωv_x

You should know from introductory physics that the motion in x-y is circular. To demonstrate that this is the case, and demonstrate the technique of change of variables to solve a differential equation, we write a new complex variable

η = v_x + iv_y.

The reason to choose this variable will become clear we we proceed -- experience led to this choice. I'll review complex numbers in a moment.

The time derivative of η is

η[dot] = v_x[dot] + iv_y[dot] = ωv_y - iωv_x = -iω(v_x + iv_y) = -iωη

With this choice of variable, we have gone from a pair of coupled differential equations to a single (complex) differential equation. Despite involving complex numbers, this equation is easily solved, as we've already done. The equation says that η is a function whose derivative is equal to the original function times a constant, and we've seen that this function is an exponential,

η = Ae^-iωt.

straightforward except that the argument of the exponential is a complex number. We'll look at what it means to have a complex exponential.