PHY5200 F07

Chapter 3: Momentum and Angular Momentum

Reading

Taylor 3.4-3.5 (today) and 3.5-4.2 (Wednesday).

Recall

Conservation of linear momentum, and center of mass.

Example:

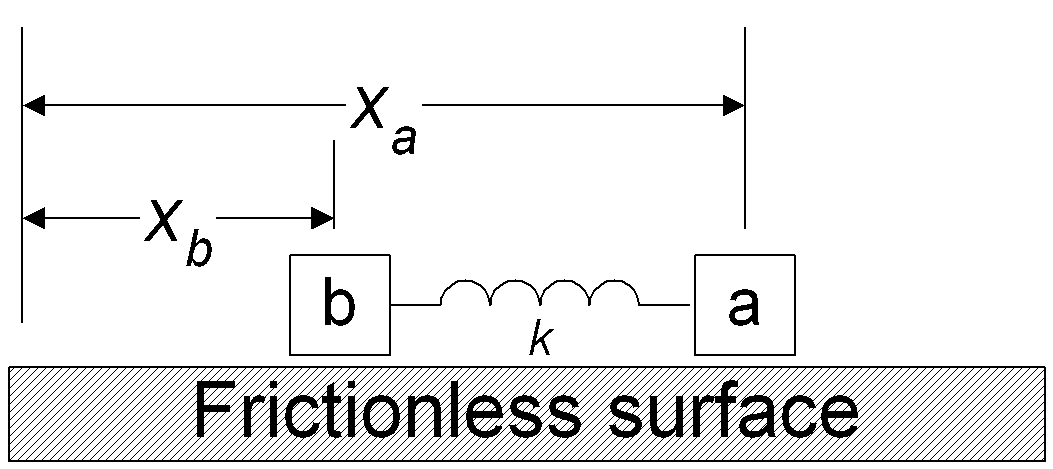
Two identical blocks, a and b, slide on a frictionless track. Each has mass m and they are attached by a spring of length l and unknown restoring force. Initially they are at rest. At t=0 block a is hit sharply giving it an instantaneous velocity v₀ away from b. Determine the motion of the CM of the blocks for all later times.

Calling the positions of a and b, x_a and x_b , the location of the center of mass is given by

x_CM = (m_ax_a + m_bx_b)/(m_a + m_b) = (x_a + x_b)/2

The position of the center of mass is halfway between the two masses, right where one would guess it should be. We can solve for the motion be separating it into the motion of the CM and the relative motion of the two blocks. Since there are no external forces on the block (apart from the initial hit that gets things moving) the momentum of the CM is constant, meaning that the CM moves with constant velocity

v_cm = p_cm/M = (mv₀/2m) = ½v₀.

If the spring is linear, with spring constant k then the relative motion of the two blocks is simple harmonic oscillation with frequency ω = (k/m)^½; we will discuss simple harmonic motion in detail in a future chapter.

Angular Momentum for a Single Particle

For a single particle, angular momentum is defined as L = r × p. Angular momentum is a vector quantity, but has the odd property that it is perpendicular to the plane of motion -- the plane containing r and p. Perhaps you recall from introductory physics that the time rate of change of L is equal to the applied torque, N = r × F. We can derive this by evaluating the time derivative of L.

The first cross product is zero because the velocity is parallel to the momentum, v × p = m(v × v) = 0.

An angular momentum usually (but not always) means that we are dealing with some sort of rotation, like a spinning wheel, or planets orbiting a sun. A rotation has a center where it is natural to place the origin of coordinates, but up to now we haven't made use of this fact. We will now, in connection with the idea of central forces. A central force is one that points along the line connecting two interacting objects. The gravitational and electrostatic forces are central forces. Friction and the Lorentz magnetic force are not. If a situation involves a central force, and we measure position from the center of force, then r and F are parallel and the torque N is zero, and the angular momentum L is constant. This is the law of conservation of angular momentum: if the applied torque is zero then angular momentum is conserved.

Kepler's Second Law

After years of careful analysis of data taken by Tycho Brahe and his assistants (one of which was Kepler), Kepler came up with three observations about the orbits of planets and comets.

1. Orbits are ellipses with the Sun located at one of the foci.
2. In moving around its orbit, a line drawn from the Sun to the object sweeps out equal areas in equal times.
3. The ratio of the square of the period to the cube of the semi-major axis is a constant for all objects orbiting the Sun.

All three of Kepler's laws are derivable from Newton's laws. (Since Newton's laws apply to objects other than planets and comets, they are considered more fundamental than Kepler's.) At this point, we can derive the second law; we will derive the remaining two in Chapter 8.

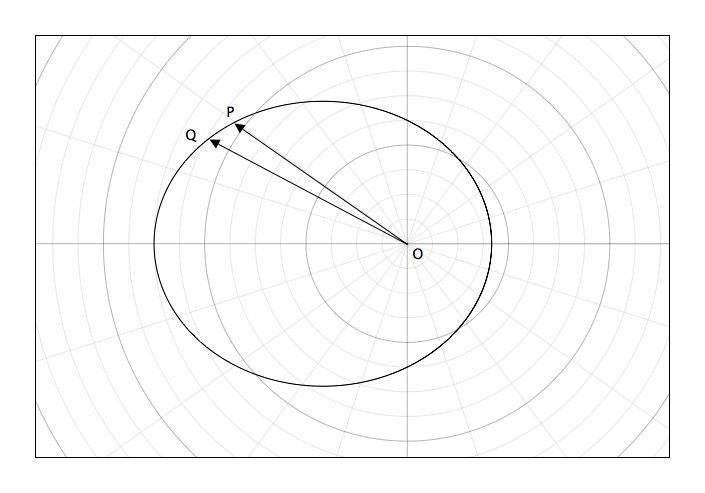
Imagine a planet orbiting the Sun, with the Sun at point O. Following the discussion in the text, consider a small part of the planet's orbit from point P to Q. If P and Q are sufficiently close, then the area swept out is just the are of the triangle OPQ

where r is the position vector of the planet at P, measured from the sun, and v is its orbital velocity at P. Using p/m = v, and then substituting the planet's angular momentum for r × p we have

Since the only (substantial) force acting on the planet is the Sun's gravity, and this force is always parallel to r, the net torque on the planet is zero, and the angular momentum is a constant. This is therefore equivalent to Kepler's second law, that dA/dt is constant.