PHY5200 F07

Chapter 3: Momentum and Angular Momentum

Reading

Taylor 3.5-4.1 (today) and 4.1-4.3 (Friday).

Recall

Angular momentum L = r × p and time rate of change of angular momentum d_tL = N^ext.

Kepler's three laws describe the orbits of planets (this is kinematics).
The first law: orbits are ellipses with the Sun at a focus.
The third law: the square of the period divided by the cube of the semi-major axis is a constant.
The second law: equal areas are swept out in equal time.
We derived the second law from the dynamics of Newton's laws with a central force.

Angular Momentum for Several Particles

We would like to derive a similar result for a system of particles. For a system of particles, we define the total angular momentum as the vector sum of the individual particle angular momenta, L_tot = ∑_i L_i = ∑_i r_i × p_i. Let's look at the time derivative of this angular momentum.

d L_tot / dt = ∑_i [ ( d r_i / dt ) × p_i ] + ∑_i [ r_i × ( d p_i / dt ) ]

= ∑_i [ r_i × (d p_i / dt ) ]

As above, we'll use Newton's second law to substitute the force on particle i for the momentum derivative term. When considering a single particle, all forces are external. This time though, we have internal and external forces. From the previous lecture we have:

d p_i / dt = F_i^tot = F_i^ext + ∑_j F_ij

Inserting this expression in the one above gives:

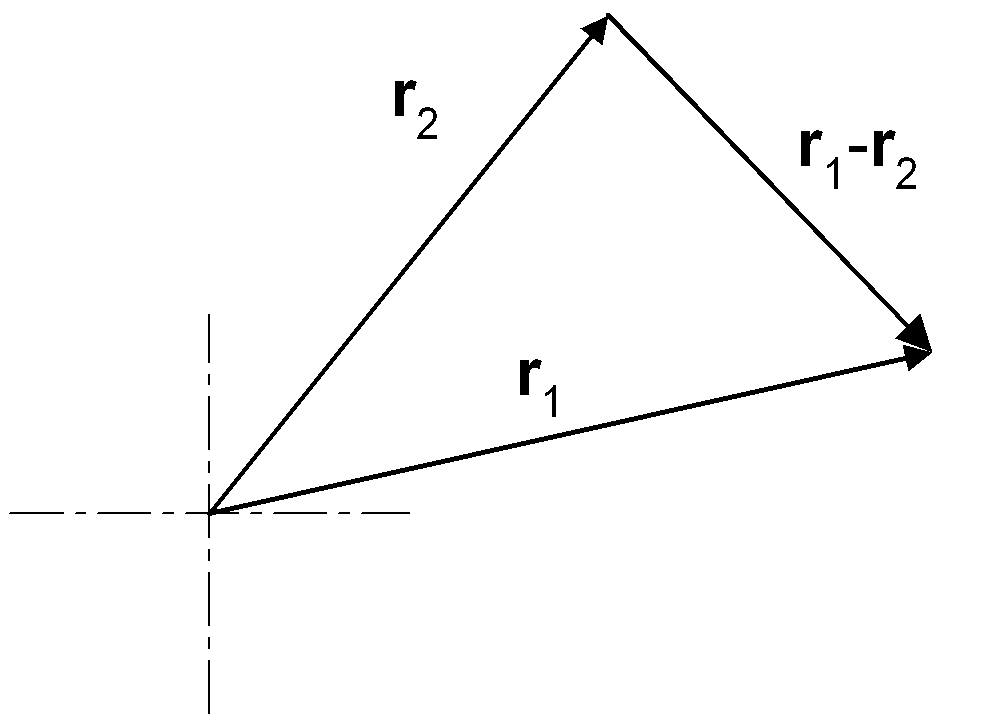
dL_tot/dt = ∑_i r_i × F_i^ext + ∑_i∑_j r_i × F_ij = ∑_i r_i × F_i^ext = N_tot

the result we wanted. The double sum of the internal forces is zero assuming that the forces between particles are central. Here's the explanation. Due to Newton's third law, for every force F_ij its pair F_ji = -F_ij. Combining these two terms yields

r_i × F_ij + r_j × F_ji = r_i × F_ij - r_j × F_ij = (r_i - r_j) × F_ij = 0

The quantity r_i - r_j is a vector pointing from particle i to particle j. If F_ij is a central force, then it also points along the line from particle i to particle j; therefore the vectors in the cross product are parallel, and the cross product is zero.

Angular momentum about the CM

Since we will often deal with the CM, it is useful to express the angular momentum in terms of the CM of the system. Recall how we used CM coordinates in the example from last lecture. Let's do that again here, r'_i = r_i - r_CM, and likewise we can express the velocity in terms of the CM velocity and the part relative to the CM.

L_tot = ∑_i (r_CM + r'_i) × m_i (v_CM + v'_i) =

L_tot = r_CM × p_CM + r_CM × ∑_i m_i v'_i + ∑_i m_i r'_i × v_CM + ∑_i m_i r'_i × v'_i =

L_tot = r_CM × p_CM + ∑_i r'_i × p'_i

To reach this solution I've used ∑_i m_i v'_i = 0 and ∑_i m_ir'_i = 0. Can you see why these are true? Hint, try calculating r_CM by expressing the coordinates in terms of the CM coordinates and the coordinate of the CM.

The above result says that the total angular momentum of a system of particles is composed of two parts: the angular momentum of the CM and the angular momentum about the CM. The second part is what we normally think of as the rotation or spinning of something. The first part we might consider as the angular momentum due to the orbit, or path of our system. This is quite a convenient occurance; the center of mass is a special point indeed.

The moment of inertia

If the object that is moving is rigid, then all the particles in the object rotate with the same angular velocity ω, and the relative position vector r'_i is perpendicular to the relative velocity vector v'_i. This is true whether measured with respect to the center of mass or any other point. With these facts, we can express the terms for the relative angular momentum as

r'_i × p'_i = m_ir'_iv'_i = m_ir'_i²ω

The sum for the angular momentum relative to the CM becomes

∑_i r'_i × p'_i = (∑_i m_ir'_i²) ω = I_CMω

where the moment of inertia is defined as

I_CM = ∑_i m_ir'_i² = ∫_volume r'² dm

Now we have an alternative way to write the total angular momentum of an object as

L_tot = r_CM × p_CM + I_CMω