PHY5200 F07
Chapter 4: Energy
Reading
Taylor 4.5-4.7 (today) and 4.7-4.9 (Friday).
Recall
F = -
Central forces are forces that act along a straight line from source to object; F = F(r)rhat.
Spherical (Polar) Coordinates
Spherical coordinates are extremely useful in central force problems: planets orbiting the sun, 3-D harmonic oscillator, or electron bound to a proton.
Spherical coordinates define a location by its
- radius from the origin, r;
- polar angle from the z axis, θ, similar to latitude on earth; and
- azimuthal angle, φ, the angle from the x axis to the projection of the location onto the x-y plane, similar to longitude on earth.
We can relate (r, θ, φ) to (x, y, z) using geometry.
First, it is easy to see that z = r cosθ.
Then the x and y components are projections of the length projected onto the x-y plane, r sinθ.
We find that x = r sinθ cosφ and y = r sinθ sinφ.
The surface of the earth is mapped with spherical coordinates with r approximately constant, so usually neglected.
The latitude is a measure of the angle from the equator (positive for north and negative for south).
This is an azimuthal angle, but measured from the equator rather than the north pole; θ = 90o - latitude.
The longitude is just like our azimuthal angle φ, where for earth we arbitrarily choose a particular direction for the x axis (φ=0).
A spherically symmetrical function f(r) means that f depends only on the distance from the origin, r, not the directions θ or φ, meaning that f(r) = f(r).
Since r, θ, and φ are independent coordinates (we can change one without changing the others), then ∂f(r)/∂θ = ∂f(r)/∂φ = 0.
Only the partial derivative with respect to r is non-zero.
The unit vectors are defined as the direction in which the corresponding coordinate increases while the other two don't change.
The unit vectors are mutually orthogonal, so the dot product of two vectors in spherical coordinates is still the sum of the products of the corresponding coordinates, that is, if a = arrhat + aθθhat + aφφhat and b = brrhat + bθθhat + bφφhat then
a⋅b = arbr + aθbθ + aφbφ.
The Gradient in Spherical Coordinates
The unit vectors rhat, θhat, and φhat aren't fixed, but change at different locations.
Therefore, care must be used when taking derivatives of vectors in spherical coordinates.
We must include the fact that the unit vectors change as well as the coordinates.
We went through this exercise for polar coordinates, and let's do it again for spherical coordinates.
If we imagine moving a small distance dr, the force will change by an amount
df = ∇f ⋅ dr
In spherical coordinates, we express a small displacement as
dr = dr rhat + rdθ θhat + r sinθ dφ φhat
Putthing these together we find
df =
Since df can also be written as the partial derivatives times infinitesimals
df = (∂f/∂r) dr + (∂f/∂θ) dθ + (∂f/∂φ) dφ
we can relate the components of the gradient to the partial derivatives to find
∇f = (∂f/∂r) rhat + (1/r)(∂f/∂θ) θhat + (1/r sinθ)(∂f/∂φ) φhat
Conservative and Spherically Symmetric, Central Forces
Spherically symmetric central forces are conservative.
Energy of Interaction of Two Particles
I have covered this in my earlier discussion of extending kinetic and potential energies to multiparticle systems.
Please read over, paying attention to the arguments about relative coordinates.
Elastic Collisions
Collisions are an important tool in physics.
Much of our understanding of the subatomic world comes from the study of collisions between subatomic particles.
Many aspects of the motion of comets and man-made satellites can be understood as "collisions" with planets and stars.
And even the physics of semiconductors and superconductors is phrased in the language of collisions.
In a collision, two objects approach each other, interact, and then continue with their motion.
We generally assume that their interaction occurs over a finite time and distance, then, even without knowing the details of their interaction (gravitational, electrical, or any other 'al) we can understand the kinematics of the collision.
The reason is conservation of momentum and energy.
- In the usual situation, there are no external forces on the two objects.
Therefore, the total momentum of the two objects is conserved.
This is always true independent of whether the forces between the objects are conservative or not.
- Total energy is conserved in the collision, but sometimes the collision process transforms some of the energy from mechanical to other forms, for instance heat.
We quantify the degree of energy conservation by the quantity ε = Δv'/Δv.
If ε=1, mechanical energy is conserved, and we say that the collision is elastic. For ε≠1, mechanical energy is not conserved, and we say that the collision is inelastic.
Elastic collisions are those where the total energy of the two particles is the same before and after the collision, Ei = Ef.
We also assume that before and after the collision, the particles are far apart, and their mutual potential energies are zero (or very small at least), so that the initial and final energies are simply the kinetic energies of the system, Ei = Ti = Tf = Ef.
Elastic collisions are especially interesting.
The elastic collision of two objects of known mass can always be treated as a two-dimensional problem (why?).
The initial kinematics are determined by the magnitudes of the two initial velocities, and the angle between the objects (3 quantities).
The final kinematics are determined by the magnitudes of the two final velocities, and two angles (another 4 quantities).
Conservation of momentum provides two constraints and conservation of energy gives a third.
So, if we know the initial conditions, we need just one piece of information about the final motion to completely solve the problem.
And even without that we can often solve for other interesting information, as illustrated by the following example.
Example: Equal-Mass Elastic Collision
Show that if two equal-mass objects collide elastically, and one of them is initially at rest, then the angle between the outgoing particles is 90o.
We have two objects of mass m, denote them as 1 and 2.
Let the first object move with inital velocity v1 = v1xhat, and final velocity v1', while the second object is initially at rest (v2 = 0), and has final velocity v2'.
Conservation of momentum implies that mv1 = mv1' + mv2' or that v1 = v1' + v2'.
Conservation of energy implies that ½mv1² = ½mv1'² + ½mv2'² or that v1² = v1'² + v2'².
These two expressions are quite close, and in fact if we square the conservation of momentum result we get v1² = v1'² + 2v1'⋅v2' + v2'².
If we subtract the expression from conservation of energy from this we're left with the result that v1'⋅v2' = 0 which is only true if either the two velocities are perpendicular, or one is zero.
Example: Another Equal-Mass Collision
Derive a relations between the sum and difference of initial and final velocities for the collision of two equal mass particles.
Make no assumptions about the velocities.
Denote the initial velocities by v1 and v2, and the final velocities by v1' and v2'.
Conservation of momentum implies that v1 + v2 = v1' + v2' which can be rewritten as
v1 - v1' = -(v2 - v2').
Conservation of energy gives v1² + v2² = v1'² + v2'² which can be rewritten as v1² - v1'² = v2'² - v2².
Further, the difference of the squares can be written as the product of the sum and the difference of the velocity vectors to yield (v1 + v1')(v1 - v1') = (v2' + v2)(v2' - v2).
Finally, we can factor out the differences using the above equality to get the result
v1 + v1' = v2' + v2.
This result is widely used in introductory physics texts.
Example: Double Ball Drop
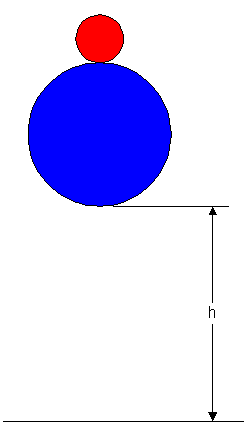Consider two balls of masses M and m, dropped together from an initial height h, where one of the balls sits directly atop the other.
The balls rebound from the floor and from each other elastically.
How far up will the upper ball bounce after they hit the floor?
Consider the special case of M >> m.
Let the ball with mass m be atop the ball with mass M.
Consider the rebound from the floor as a two separate collisions, first the lower ball (M) collides with the floor and rebounds, then the two balls collide with each other.
These two collisions are separated by an infinitisimal time, but this is the easiest way to break the problem into a set of one-on-one collisions.
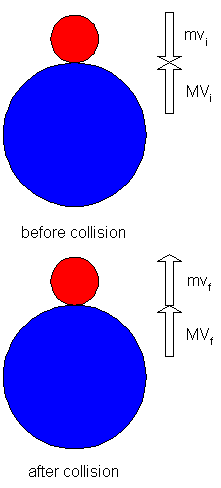Both balls fall with the same acceleration, so just before the collisions occur both balls have the same downward velocity, vi = -sqrt(2gh).
The lower ball (M) collides elastically with the floor, and rebounds with an equal but opposite velocity Vi = sqrt(2gh).
Next, the two balls collide, the lower ball (M) now moving upward with velocity Vi = sqrt(2gh), and the upper ball (m) moving downward with velocity vi = -sqrt(2gh).
Call the final velocities Vf for the lower ball (M) and vf for the upper ball (m).
Conservation of momentum gives MVi + mvi = MVf + mvf, and conservation of energy gives ½MVi² + ½mvi² = ½MVf² + ½mvf².
The first expression can be rewritten to give M(Vi - Vf) = m(vf - vi), and the second can be written as M(Vi² - Vf²) = M(Vi - Vf)(Vi + Vf) = m(vf² - vi²) = m(vf - vi)(vf + vi), and making use of the rewritten first expression this becomes (Vi + Vf) = (vf + vi).
Now let's use the fact that vi = -Vi.
With this, the first relation can be written (M-m)Vi = MVf + mvf, and the second becomes 2Vi = vf - Vf.
Use the second to eliminate Vf from the first and find (3M-m)Vi = (M+m)vf, or finally the desired result vf = Vi(3M-m)/(M+m).
Unless m > 3M, this final velocity is upward and the upper ball will rebound to a height hf = vf²/2g = h[(3M-m)/(M+m)]²
For the special case that M >> m, the result becomes hf = 9h, that is, for the case that the upper ball is much less massive than the lower ball, it rebounds to 9 times the height it was dropped from.
This is a rather surprising result and can be readily demonstrated -- but be careful of people, lights, and the ceiling!
This result also has application to supernova explosions.
When a massive star burns as much of its fuel as possible, it stops fusing nuclei, and stops generating energy in its core.
The temperature of the core drops, and the pressure in the core decreases.
That pressure previously counteracted the gravitational weight of the overlying material, and when it decreases, the star collapses under its own weight.
The outer material of the star collides with the small, dense core, and rebounds with enormous speed, like the upper ball in this example.
The whole process happens so quickly that the rebounding material creates an explosion.
© 2007 Robert Harr