PHY5200 F07

Example: Another Equal-Mass Collision

Derive a relations between the sum and difference of initial and final velocities for the collision of two equal mass particles. Make no assumptions about the velocities.

Denote the initial velocities by v₁ and v₂, and the final velocities by v₁' and v₂'. Conservation of momentum implies that v₁ + v₂ = v₁' + v₂' which can be rewritten as

Conservation of energy gives v₁² + v₂² = v₁'² + v₂'² which can be rewritten as v₁² - v₁'² = v₂'² - v₂². Further, the difference of the squares can be written as the product of the sum and the difference of the velocity vectors to yield (v₁ + v₁')(v₁ - v₁') = (v₂' + v₂)(v₂' - v₂). Finally, we can factor out the differences using the above equality to get the result This result is widely used in introductory physics texts.

Example: Double Ball Drop

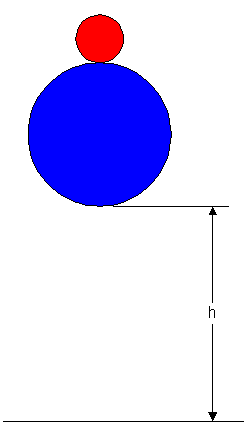Consider two balls of masses M and m, dropped together from an initial height h, where one of the balls sits directly atop the other. The balls rebound from the floor and from each other elastically. How far up will the upper ball bounce after they hit the floor? Consider the special case of M >> m.

Let the ball with mass m be atop the ball with mass M. Consider the rebound from the floor as a two separate collisions, first the lower ball (M) collides with the floor and rebounds, then the two balls collide with each other. These two collisions are separated by an infinitisimal time, but this is the easiest way to break the problem into a set of one-on-one collisions.

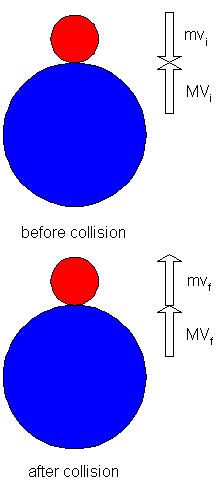Both balls fall with the same acceleration, so just before the collisions occur both balls have the same downward velocity, v_i = -sqrt(2gh). The lower ball (M) collides elastically with the floor, and rebounds with an equal but opposite velocity V_i = sqrt(2gh).

Next, the two balls collide, the lower ball (M) now moving upward with velocity V_i = sqrt(2gh), and the upper ball (m) moving downward with velocity v_i = -sqrt(2gh). Call the final velocities V_f for the lower ball (M) and v_f for the upper ball (m). Conservation of momentum gives MV_i + mv_i = MV_f + mv_f, and conservation of energy gives ½MV_i² + ½mv_i² = ½MV_f² + ½mv_f². The first expression can be rewritten to give M(V_i - V_f) = m(v_f - v_i), and the second can be written as M(V_i² - V_f²) = M(V_i - V_f)(V_i + V_f) = m(v_f² - v_i²) = m(v_f - v_i)(v_f + v_i), and making use of the rewritten first expression this becomes (V_i + V_f) = (v_f + v_i).

Now let's use the fact that v_i = -V_i. With this, the first relation can be written (M-m)V_i = MV_f + mv_f, and the second becomes 2V_i = v_f - V_f. Use the second to eliminate V_f from the first and find (3M-m)V_i = (M+m)v_f, or finally the desired result v_f = V_i(3M-m)/(M+m). Unless m > 3M, this final velocity is upward and the upper ball will rebound to a height h_f = v_f²/2g = h[(3M-m)/(M+m)]²

For the special case that M >> m, the result becomes h_f = 9h, that is, for the case that the upper ball is much less massive than the lower ball, it rebounds to 9 times the height it was dropped from. This is a rather surprising result and can be readily demonstrated -- but be careful of people, lights, and the ceiling!

This result also has application to supernova explosions. When a massive star burns as much of its fuel as possible, it stops fusing nuclei, and stops generating energy in its core. The temperature of the core drops, and the pressure in the core decreases. That pressure previously counteracted the gravitational weight of the overlying material, and when it decreases, the star collapses under its own weight. The outer material of the star collides with the small, dense core, and rebounds with enormous speed, like the upper ball in this example. The whole process happens so quickly that the rebounding material creates an explosion.

Example: A Cylinder Rolling Down a Hill

We analysed this problem using forces and equations of motion earlier. Now, let's treat the problem using energy.

Consider a cylinder (mass M, radius R, and I = ½MR²) starts from rest and rolls without slipping down a hill of arbitrary construction -- just that it goes downhill. What is the velocity of the cylinder after it descends a height h?

Since the cylinder rolls without slipping, it doesn't lose any energy to friction, so the total mechanical energy of the cylinder is conserved. Its mechanical energy is the sum of gravitational potential energy and kinetic energy. Since the cylinder starts from rest, the initial energy is purely gravitational potential energy, E_i = U = Mgh_i, where h_i is the initial height. The final energy is E^f = T + U = ½Mv² + ½Iω² + Mgh_f. For a rolling cylinder (or wheel), ω = v/R. Equating initial and final energies, we have Mgh_i = ½Mv² + ¼Mv² + Mgh_f = (3/4)Mv² + Mgh_f, and solving for v gives

Where Δh = h_i - h_f is the difference between the initial and final heights. Notice that the details of the shape of the hill are not needed.