PHY5200 F07

Chapter 5: Oscillations

Reading

Taylor 5.3 (today) and 5.4-5.5 (Wednesday).

Recall

Any problem with a linear restoring force (arises in most small amplitude approxmations) has harmonic oscillation as its solution. We've discussed 4 forms for writing the solution.

if there is a linear restoring force in N directions, we have an N-dimensional harmonic oscillator.

Anisotropic Oscillator

If ω_x/ω_y is a rational number, then the motion is periodic (i.e. the mass will eventually return to its initial position with its initial velocity and completely retrace the path it took to get there. If the ratio is irrational, then the motion never repeats.

One More Example of Small Oscillations

What is the frequency for small oscillations of a mass m about the minimum of the potential U(r) = a/r ² - b/r ?

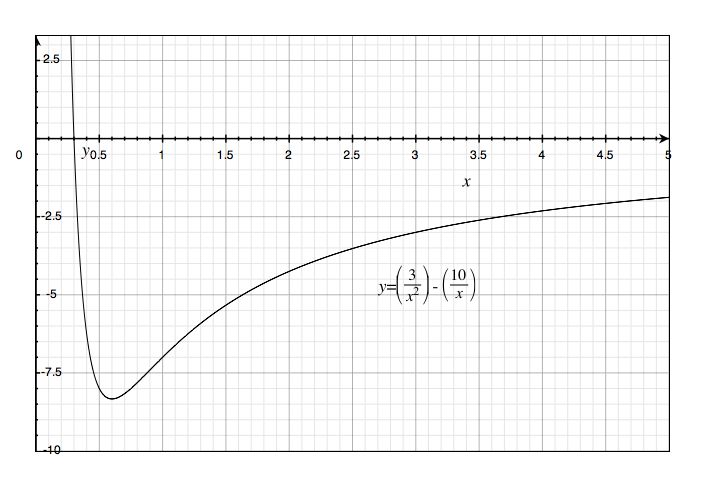
An example of this potential for a=3 and b=10 is displayed above. First, find the minimum of the potential.

∂U/∂r = b/r ² - 2a/r ³ = 0

thus r_min = 2a/b. The value of the potential at this minimum is U(r_min) = b ²/4a - b ²/2a = -b ²/4a.

Second, to determine the frequency for small oscillations, we need the second derivative of U at the minimum.

∂²U/∂r ²)_rmin = 6a/r ⁴ - 2b/r ³ = b ³/8a ³(3b - 2b) = b ⁴/8a ³.

The second derivative is positive, so this is a position of stable equilibrium. In the small amplitude approximation, this is the equivalent of k, giving

ω₀ = Sqrt(k/m) = Sqrt(b⁴/8a³m) = (b²/2a) (2am)^-½.