PHY5200 F07

Chapter 5: Oscillations

Reading

Taylor 5.4-5.5 (today) and 5.5-5.6 (Friday).

Recall: Summary of the SHO:

Spring-like force: F = -kx
Energy conservation, potential energy U = ½kx ²
Undamped or natural frequency ω₀ = Sqrt(k/m)
General solution x = Asin(ω₀t + φ)
Addition of a constant force changes the equilibrium position, but not the results of the general solution.
Any potential with a "parabolic" minimum has a SHO solution for small oscillations (for example, the simple pendulum or the example from Monday).

Damped Oscillations

m d_t² x = -kx - b d_t x

m d_t² x + b d_tx + kx = 0

Damped Harmonic Oscillator

Now let's apply a new technique to the important problem of the damped harmonic oscillator. We assume that the damping (resistance) term is linear in the velocity. This makes the problem possible to solve in closed form, but in this case, it is also an important example with interesting behavior to understand.

m d_t²x + b d_tx + kx = 0

There are a number of ways to solve DE's, for instance direct integration, "guessing" the solution, or the method of operators that I will demonstrate here. Let D stand for the "operation" of taking a derivative (a time derivative for our purposes). Then a_x = Dv_x, and v_z = Dz. With this notation, the above differential equations become:

mD²x + bDx + kx = 0

Let β = b/2m, ω₀² = k/m, and divide through by m to get:

(D² + 2βD + ω₀²)x = 0

This equation looks like a second order polynomial. A second order polynomial can always be factored (allowing for the use of imaginary numbers) and it turns out that we can do the same with our operator expression because none of the terms in parenthesis (all constants) are effected by the derivative operation (we say they commute).

[D +β - (β² - ω₀²)^½][D + β + (β² - ω₀²)^½]x = 0

The order of the two terms is arbitrary. Clearly if the result of the first (rightmost) term in brackets is zero, then the equation is satisfied. But we have solved this earlier, and the solution is an exponential function. The same holds here. Let's call the quantity β² - ω₀² = q². Then there are two solutions for x:

x = A_± exp[-(β±q)t]

This result may seem a bit strange at first. After all, in the undamped case, the solution was a sine or cosine function not an exponential, and letting β-->0 takes us to the undamped case. What happens when β=0? Then q²=-ω₀² leading us to conclude that q is imaginary. And x is the exponential of an imaginary number times t, i.e. the solution becomes a sine or cosine function.

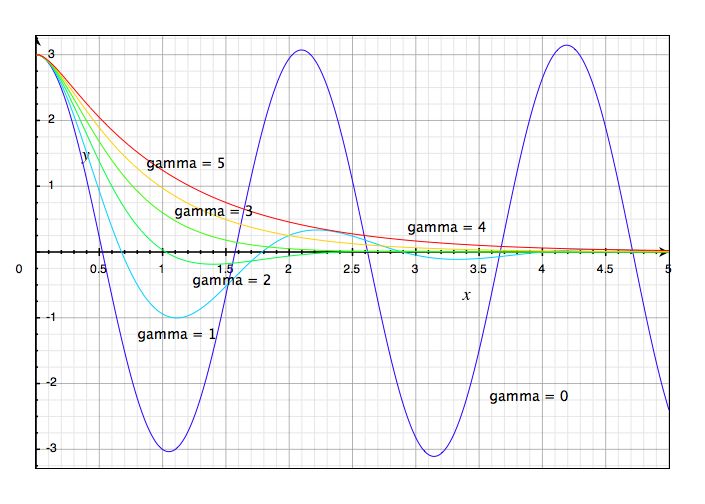
Recall that q² = β² - ω₀². Then we have 3 cases to consider:

q² > 0 This situation is called overdamped.
q² = 0 This situation is called critically damped.
q² < 0 This situation is called underdamped.

Overdamped

This is mathematically the easiest case. The solution is:

x(t) = A₁e^-(β-q)t + A₂e^-(β+q)t

v(t) = -(β-q)A₁e^-(β-q)t - (β+q)A₂e^-(β+q)t

This solution corresponds to the position returning exponentially to the equilibrium position. Despite the name "damped harmonic oscillation", there is no oscillation! Well, if you arrange things right there might be one oscillation.

And note that q is always less than γ, so it is never possible for β-q to become negative and therefore turn the A₁ exponential into a positive exponential.

Critically Damped

When q=0, the two terms of the DE are identical:

[D + β] [D + β]x = 0

So the solution x₁ = Ae^-βt has only one arbitrary constant. But this is a second order DE -- there should be TWO arbitrary constants. Physically this corresponds to being able to independently specify the initial position and velocity for the oscillator. The solution to this dilema is to ask if there is a function x₂(t) that yields a result of the form Ae^-βt after being acted on by [D + β]. Then the second [D + β] guarantees that the result is 0. Mathematically this means:

[D + β] x₂(t) = Ae^-βt

The solution, which can be verified by substitution, is

x₂(t) = Ate^-βt

So, our general solution for the critically damped case is the sum of x₁ and x₂:

x(t) = Ate^-βt + Be^-βt = (At + B)e^-βt

v(t) = (A - βB - βAt)e^-βt

Underdamped

When q² < 0, the solution to the DE is an exponential with a complex exponent. Recall that e^iθ = cosθ + isinθ. The solution is then:

x(t) = e^-βt [Csin(ω_dt) + Dcos(ω_dt)] = e^-βt Acos(ω_dt + δ)

v(t) = -Ae^-βt [βsin(ω_dt + δ) - ω_dcos(ω_dt + δ)]

These two forms of the solution are equivalent. In the first case, C and D are the unknown constants while in the second case they are A and δ. The frequency ω_d = iq = (ω₀² - β²)^½ = (k/m - c²/4m²)^½ and is called the damped frequency (ω₀ is the undamped or natural frequency).

This solution is almost the same as the solution of the undamped oscillator. There are two differences:

The amplitude decays exponentially to zero, and
the frequency of oscillation is ω_d rather than ω₀.