Taylor 8.3-8.5 (today) and 8.5-8.7 (Friday).
But notice that the relative coordinates are really the same vector with different scaling
where I've used r12 = r2 - r1. Now it is easy to see that the two equations of motion for the relative coordinates are actually the same equation written in terms of the separation vector r:
And even more fortuitously, the force is also a function of just the separation distance between the two objects. So, the two original equations of motion in terms of r1 and r2 transform into two nicer equations, one in terms of the CM coordinate R and the other in terms of the separation vector r12 which I'll call simply r from now on.
The quantity m1m2 / M has the units of mass and is called the reduced mass of the system, μ = m1m2 / (m1 + m2). The reduced mass has some interesting properties. It is always less than either of the original masses, μ < m1 and μ < m2. If one mass is much greater than the other, say m1 << m2, as happens with the earth orbiting the sun, or an electron orbiting a nucleus, then the reduced mass is approximately equal to the smaller mass, μ ≅ m1. If the two original masses are equal, then the reduced mass is just half the mass of either, m1 = m2 = m, then μ = m/2. And, if one mass is fixed, or if the problem involves just one mass and a fixed origin of force, then this solution is directly applicable, simply by setting the mass of the moving object equal to μ.
Using the reduced mass, the equations of motion read
and
where
In chapter 3 we learned that when objects interact only by a central force, their angular momentum is conserved. To demonstrate this, let's look at various angular momenta in this problem, and their time derivatives. Consider the angular momenta of object 1 and object 2 relative to the center of mass:
and the angular momentum of the center of mass
The time derivatives of these are:
So all three of these angular momenta are conserved. The conservation of the center of mass angular momentum will be mainly ignored, except to point out that it doesn't mean that the CM rotates around the orgin of coordinates. This would contradict the result that the total momentum vector is conserved. Rather, it is just that R × P is constant, and this can occur for straight line motion (draw a figure).
More important to us is that the individual angular momenta about the CM are conserved. And both point in the same direction as we can see by writing the relative position and momentum vectors in terms of the separation vector r:
Therefore, relative to the CM, the objects move in the plane perpendicular to angular momenta. The total angular momentum is the sum of the individual angular momenta
This is the expression for the angular momentum of a particle of mass μ with coordinates r and velocity dtr.
Let's also look at the energy ... This again confirms that using the reduced mass and relative separation allows us to treat the problem in a general manner, and the solution can be applied to a number of different circumstances.
We will now make use of this fact to write the equation of motion in a particular coordinate system, namely cylindirical polar coordinates. Since the motion occurs in a plane, cylindirical polar coordinates with the CM as origin, and the z axis aligned with the angular momentum vector, perpendicular to the plane of motion. With this choice, the motion occurs in the r-φ plane; there is no motion in the z direction. Of course, I'm speaking of the motion relative to the CM, the CM can move in the z direction so that objects move in the z direction. In cylindrical polar coordinates, the equation of motion separates into three equations, one in r, one in φ, and one in z:
The equation in z is written for completeness, but simply expresses the fact that there is no motion in z (zero acceleration means constant velocity, but since the initial velocity is zero, there is no motion in z).
The angular momentum is constant. It is useful to evaluate those in polar coordinates as well.
I've used the symbol l to represent the total momentum (relative to the CM) of the system. From this expression, we can solve for dtφ in terms of r, dtφ = l/μr², and use this to simplify the r and φ equations of motion.
The r equation can be rewritten in the form
where I've introduced the effective potential Ueff = U(r) + l²/2μr² in order to make this look like a one-dimensional problem of motion in r subject to this effective potential. If we multiply both sides of this expression by dtr, then each side is seen to be a time derivative:
therefore
The quantity in parentheses is the energy in the CM system, and this says that the energy is constant.
Below we show Ueff versus r for several potentials, ½kr², -k/r
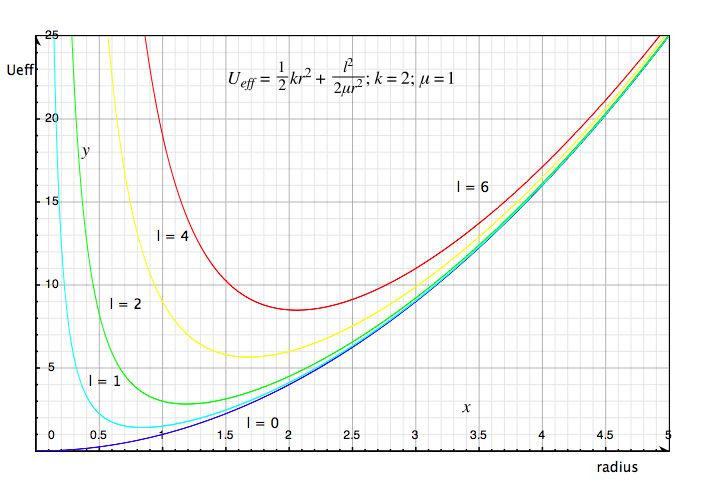
The graph shows the effective potential for a spring force, F = -kr. The curves are for different angular momenta. Increasing angular momentum causes the minimum of the potential to move to greater radius.
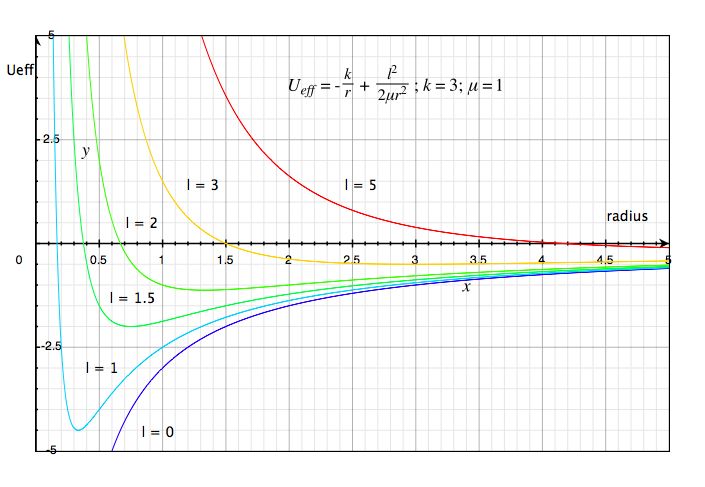
The above graph shows the effective potential for a gravitational force, F = -k/r². The curves are for different angular momenta. Increasing angular momentum causes the minimum of the potential to move to greater radius. Note that as r goes to infinity, the effective potential goes to zero, so any curve that crosses zero at a finite radius has bound orbits, that is, all curves shown. But for l = 0, the system passes through zero separation (radius).
The expression now looks like a one-dimensional kinetic energy in the coordinate r, with the effective potential Ueff = U(r) + l²/2μr².