Taylor 11.2-11.3 for today and 11.4-11.6 for Friday.
We will now solve some example coupled oscillator problems. To keep this first problem simple, we'll look at the model system with both masses equal, m1 = m2 = m, and idential spring constants k1 = k2 = k3 = k. The matrix M becomes m1, where 1 is the unit matrix, and K becomes k[(2, -1), (-1, 2)]. The determinant expression becomes
The solutions (eigenvalues) are ω² = 3k/m and ω² = k/m. The normal frequencies are ω1 = &radic(k/m) and ω2 = &radic(3k/m). They are the frequencies at which both carts can oscillate simultaneously -- pay attention to the in-class demonstration with coupled pendula.
To understand what this means, let's complete the picture by determining the eigenvectors for these eigenvalues. The eigenvectors are the values of C that satisfy the eigenvalue equation (K - ω²M)C = 0 for a particular eigenvalue. First let's take ω = ω1 = &radic(k/m). The eigenvalue equation reads
where C1 and C2 are the two components of C. The solution has C1 = C2, so a normalized eigenvector is C1 = √(½) [1, 1]. The position vector is
Now let's take ω = ω2 = &radic(3k/m). The eigenvalue equation reads
The solution has C1 = -C2, so a normalized eigenvector is C2 = √(½) [1, -1]. The position vector is
The most general motion is a linear combination of these two solutions. Notice that C1 and C2 are orthoganol column matrices ("vectors"), that is C1TC2 = C2TC1 = ½ - ½ = 0. Therefore, they can be thought of as basis vectors in the two dimensional space of the coordinates x1 and x2. Any possible solution can be expressed as a linear combination of our two eigenvector solutions.
So we see that it isn't possible for one cart to move and not the other, that is, it isn't possible to vary x1 without also varying x2. Certain combinations of coordinates do have this property, and they are called normal coordinates. Normal coordinates correspond to combinations of the physical coordinates, and always exist in problems such as this.
In this case, we can replace x1 and x2 by
and
These coordinates are orthogonal, and therefore span the space of all possible values for x1 and x2. For this simple example, it is relatively easy to see that ξ1 corresponds to the first eigenvector and ξ2 to the second, so that for the first normal mode
and for the second
Only ξ1 oscillates in the first normal mode and only ξ2 in the second (of course physically, both masses move, but in the manner dictated by the linear combinations yielding ξ1 and ξ2). The general motion can be written as a linear combination of these two coordinates. One can think of the motion of the system as composed of the motions of each cart individually, or as composed of the motions in each normal mode, where each normal mode represents a particular coordination of the motions of the two carts (a dance if you will).
Another situation of particular interest occurs when a set of (identical) harmonic oscillators are coupled, but only weakly. This is a technique commonly applied to solving problem: if you have a difficult problem that involves two simpler situations, that you do know how to solve, coupled together, first consider the problem with weak coupling. In our simple model, this situation would correspond to the case of two equal masses, and identical springs 1 and 3, k1 = k3 = k, and a much weaker spring coupling them, k2 << k. This implies that at some point we will make an approximation and drop terms that are small.
Before beginning, we expect to find solutions that are close to two uncoupled oscillators. There will be some small effect due to the weak coupling.
The matrix M is unchanged from before, and we can now write K as K = [((k + k2), -k2), (-k2, (k + k2))]. The determinant equation becomes
The two normal mode frequencies are
Thus far we've made no approximations.
In the weak coupling limit (k2<
Now we can write the two normal frequencies as being a little below and a little above the average frequency ω0
where some calculation will reveal that ε ≈ k2)/2m.
The actual motion is the real part of x. This gives
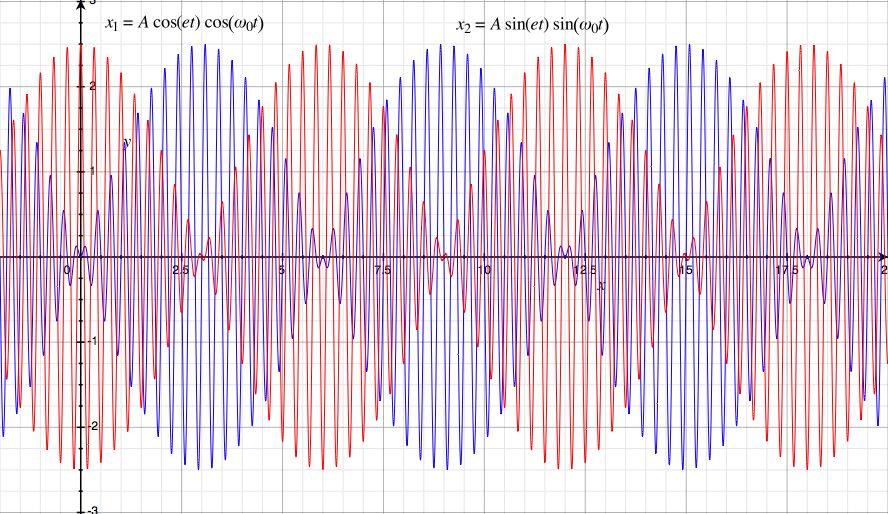
Let's look at this result in detail. Since ε << ω we can consider the factors A cosεt and A sinεt as a slowly changing amplitude for the cosωt and sinωt oscillations. That is, we can approximate the overall motion as (rapid) oscillations at the uncoupled frequency occurring with an envelope of slowly varying amplitude. The amplitude envelopes vary out of phase, so that first mass 1 swings at full amplitude while mass 2 is at rest; then the energy in mass 1 is transferred to mass 2, with a corresponding increase of the amplitude of mass 2 and reduction of amplitude of mass 1; until finally mass 2 swings at full amplitude and mass 1 comes to rest; then the whole process repeats but with energy being transferred from mass 2 to mass 1.
This phenomenon is known as beats. It arises when two modes exist that are close in frequency. It occurs with sound waves, electrical waves, and quantum mechanical probability waves.
© 2008 Robert Harr