In Taylor, read sections 11.3 to 11.4 for today, and 11.5 for Wednesday.
For two masses and three springs we found
where M is the diagonal matrix [(m1, 0), (0, m2)] and K is the matrix [((k1 + k2), -k2), (-k2, (k2 + k3))].
Another situation of particular interest occurs when a set of (identical) harmonic oscillators are coupled, but only weakly. This is a technique commonly applied to solving problem: if you have a difficult problem that involves two simpler situations that you do know how to solve, coupled together, first consider the problem with weak coupling. In our simple model, this situation would correspond to the case of two equal masses, and identical springs 1 and 3, k1 = k3 = k, and a much weaker spring coupling them, k2 << k. This implies that at some point we will make an approximation and drop terms that are small.
Before beginning, we expect to find solutions that are close to two uncoupled oscillators. There will be some small effect due to the weak coupling.
The matrix M is unchanged from before, and we can now write K as K = [((k + k2), -k2), (-k2, (k + k2))]. The determinant equation becomes
This equation yields two normal mode frequencies
and
Thus far we've made no approximations. In the weak coupling limit, k2 << k, we find two normal frequencies that are nearly equal, as suggested at the beginning. The first frequency is the same as in the first example, and the same frequency we would expect for two independent, but identical, oscillators. The effect of the weak coupling is expressed in the second frequency ω2 being slightly higher than the uncoupled frequency. It is convenient to express this result in a different way that emphasizes the closeness of ω1 and ω2. Start by taking the average of ω1 and ω2
Now we can write the two normal frequencies as being a little below and a little above the average frequency ω0
where some calculation will reveal that ε ≈ k2/2m.
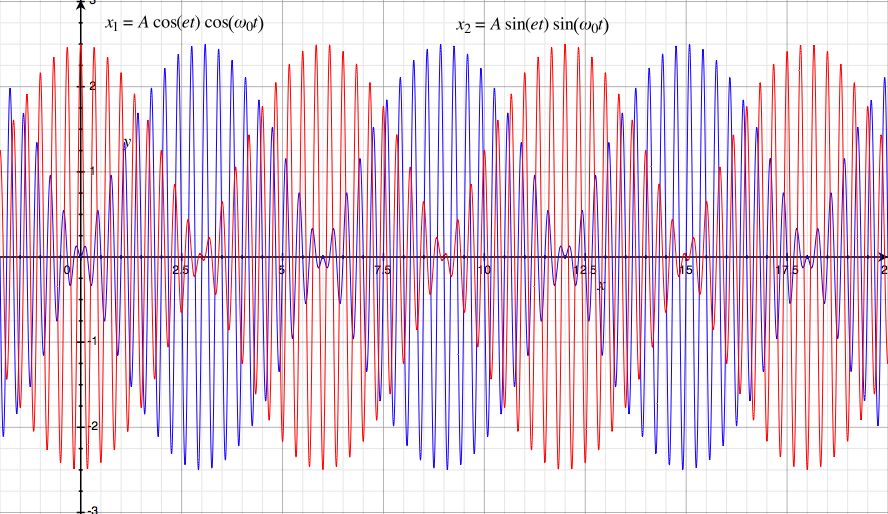
The actual motion is the real part of x (or equally valid, the imaginary part). Taking the real part gives

Let's look at this result in detail. Since ε << ω we can consider the factors A cos εt and A sin εt as a slowly changing amplitude for the cosωt and sinωt oscillations. That is, we can approximate the overall motion as (rapid) oscillations at the uncoupled frequency occurring with an envelope of slowly varying amplitude. The amplitude envelopes vary out of phase, so that first mass 1 swings at full amplitude while mass 2 is at rest; then the energy in mass 1 is transferred to mass 2, with a corresponding increase of the amplitude of mass 2 and reduction of amplitude of mass 1; until finally mass 2 swings at full amplitude and mass 1 comes to rest; then the whole process repeats but with energy being transferred from mass 2 to mass 1.
This phenomenon is known as beats. It arises when two modes exist that are close in frequency. It occurs with sound waves, electrical waves, and quantum mechanical probability waves.
A double pendulum is a pendulum suspended from a pendulum. Call the upper mass m1, the lower mass m2, the length of the upper pendulum is L1 and the length of the lower pendulum is L2. The upper pendulum hangs at an angle φ1 to the vertical and the lower makes an angle φ2 to the vertical.
As is the case for the single pendulum, it is possible to analytically solve for the motion only in the case of small angle oscillations, so we will make the small angle approximation.
The potential energy of the upper pendulum is
The potential energy of the lower pendulum is
In the small angle approximation, the total potential energy is
For the first mass, the position is (x1, y1) = L1 (sinφ1, 1-cosφ1), and the kinetic energy is T1 = ½ m1 L1² φ1dot².
The position of the second mass is (x2, y2) = (x1, y1) + L2 (sinφ2, 1-cosφ2). The square of the velocity is v2² = x2dot² + y2dot² = L1² φ1dot² + L2² φ2dot² + L1 L2 φ1dot φ2dot (cosφ1 cosφ2 + sinφ1 sinφ2). The final trigonometric terms can be written as cos(φ1 - φ2) ≈ 1 for small angles.
Putting these together, we can write the kinetic energy as
And the Lagrangian is T - U. Lagrange's equations yield, for φ1
and for φ2
These can be written in our standard matrix form
where
and
and
Try the same trick again to solve this equation: try the solution φ = aeiωt, and get the characteristic equation (K - ω² M) a = 0 which must be solved for ω and a.
As a simple example, consider the case when the masses and lengths are equal. This simplifies K and M to
and
where ω0 = √(g/L) is the natural frequency of a pendulum of length L. The characteristic equation (determinant) is
This has solutions
The normal modes are found by substituting back into the characteristic equation. For ω1 we get
implying that a2 = √2 a1. For ω2 we get
implying that a2 = -√2 a1.
In the first mode, the masses oscillate together, but the amplitude of the lower mass is √2 times larger than the amplitude of the upper mass. In the second mode, the masses oscillate 180° out of phase, again with the lower mass swinging with an amplitude √2 times greater than the upper mass.
![]()