In Taylor, read sections 14.1 to 14.2 for today, 14.3 to 14.4 for Wednesday.
Two of the most important tools for studying phenomenon are oscillations and scattering. We studied simple harmonic, damped, and forced oscillations in chapter 5, and coupled oscillators in chapter 11. Now we will study scattering, learning concepts like impact parameter and cross section, and lookint at the details of a seminal scattering experiment carried out by Ernest Rutherford and his team.
Many phenomena can be viewed as scattering problems: a comet passing near the sun; a meteor entering earth's atmosphere; or the collision of billiard balls. The prototypical scattering experiment involves objects at the atomic scale or below, i.e. nuclei or subatomic particles. In such experiments, the orbit of the projectile around the target cannot be known in detail, both because we can't know the position of projectile and target with sufficient accuracy, and because of quantum mechanical limitations. Instead, we imagine many projectiles randomly distributed with respect to the target, and ask with what probability the projectile will scatter in a particular direction. This approach takes some getting used to.
The prototypical model of a collision experiment (whether with subatomic particles or billiard balls) is a projectile approaching a stationary target from a great distance where its initial motion is unaffected by the target. More precisely, initially the projectile-target system is assumed to have zero potential energy, so the initial energy of the system is just the kinetic energy of the projectile. The projectile approaches the target is is deflected by their interaction. The projectile (and sometimes the target as well) is scattered, and moves away, where again the potential energy of interaction approaches zero, so the final energy of the system is again purely kinetic (though it could be the kinetic energy of both projectile and target).
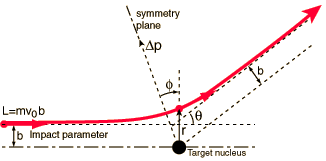
The angle between the final and initial velocities of the projectile is called the scattering angle θ. The angle θ = 0 means there was no scattering, the projectile moved along a straight line. The maximum scattering angle is θ = π, meaning that the projectile bounced straight back from the target.
The inpact parameter, b, is the closest distance the projectile would approach the target if it moved without deflection. In subatomic scattering experiments, it is impossible to know the impact parameter a priori, so this is the quantity that we average over when determing the probability to scatter in a particular direction. The minimum impact parameter is b = 0, corresponding to a head-on collision. The larger the impact parameter, the more the projectile misses the target, normally yielding smaller scattering angles.
A basic assumption is one-to-one correspondence between impact parameter and scattering angle -- that a particle scattered in a particular direction had a particular impact parameter. So, first we need to find the relation between impact parameter and scattering angle, and then average over the possible impact parameters to find the probability for scattering in a particular direction.
Experimentally, it is easy to measure the scattering angle, while basically impossible to measure the impact parameter directly.
Since we can't measure the trajectories of projectile and target well enough to predict if a collision will occur in subatomic processes, we generate a probability. The apparent size of the target is called the cross section.
The number of collisions that occur must be proportional to the number of incident projectiles, the number of targets, and the collision cross section. To determine the number of collisions (scatters), we assume that the targets don't overlap, and that the incident projectiles (beam) intercepts a finite area of the target assembly, that is, the target assembly (the sum of all the individual target atoms, nuclei, or whatever) is much larger than the beam. Now draw some area around the region where a projectile is incident on the target assembly. This area can be of any convenient shape, say it is a square of area A = 1 mm². The number of targets in this square is the density of targets times the area, Ntar = ntarA where N is a number and n is a density (number per unit area). Since the targets don't overlap, the cross sectional area where a collision can occur is σ Ntar = ntar σ A. The probability that a given incident particle scatters equals the fraction of the time that it lands within the cross sectional area of a target, which is the fraction of the area A occupied by targets, or Psc = σ Ntar/A = ntar σ. The total number of scatters is the total number of incident projectiles times the probabiltiy for one of them to scatter,
By dividing both sides by Δt, we can find the rate of scatterings in terms of the rate of incoming projectiles, often an interesting quantity,
A spacecraft is being sent through the asteroid belt on a straight, unguided trajectory. If the typical radius of asteroids is 3m and their density is 1/km² (totally fabricated numbers), and the spacecraft is 1m in radius, what is the probability that the spacecraft will hit an asteroid?
The typical cross section for a collision between the spacecraft and an asteroid is σ = π(Rast + Rcft)² = 50m². The density of targets is ntar = 1/km² = 10-6/m². The probability of a collision is Psc = ntar σ = (10-6/m²)(50m²) = 5×10-5.
In nuclear and particle physics, the targets are rather small, and m² is an awkward unit for cross section. The unit commonly used is the barn where 1 barn = 1b = 10-28m². The cross section of an atomic nucleus is approximately 1 barn. Many processes have much smaller cross sections, millibarns (mb), microbarns (μb), picrobarns (pb), and femtobarns (fb) are often encountered.
![]()