In Taylor, read sections 14.3 to 14.4 for today, 14.5 to 14.6 for Friday.
The relation between the number of scattered particles, the number incident, the target density, and the target/projectile cross section is
It is possible to generalize the formula for the number of scattered particles for cases where there are different processes (other than elastic scattering), and even different targets mixed together.
As used in the example above, the cross section for the scattering of two hard spheres of radii R1 and R2 has cross section σ = π(R1 + R2)². Note that the cross section depends on properties of both the target and the projectile.
The definition for cross section was for an elastic scattering, a process where the objects that emerge from the collision are the same as the initial projectile and target. But there are many other types of processes in which the projectile, target, or both are changed by the collision. For example, we can imagine scattering electrons off an atom in its ground state. If the final particles are just an electron and the atom, still in its ground state, then the scattering was elastic. But many other processes are also possible:
We can assign a cross section to each process, and sum them to get the total cross section for a collision: σtot = σelastic + σphoton + σion + σcap. The number of captures is the given by Ncap = Nincntarσcap, and the total number of collisions of any sort is Ntot = Nincntarσtot.
In the definition of the scattering cross section, we counted any scattering. It is possible to be more specific, and ask how many scatterings occur in a particular direction. We imagine a cone with its apex at the target as defining a region into which we will count the number of scattered particles.
We will need to define a quantity called the solid angle that characterizes the size of the cone defining the region in 3--dimensions. The definition is made in analogy to an angle in 2--dimensions. In 2--dimensions, we define the angle between 2 lines as θ = s/r where r is the radius of a circle centered at the intersection of the lines, and s is the arc length subtended between the lines.
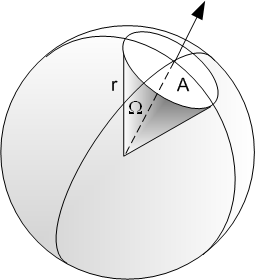
In 3--dimensions we define the solid angle of a cone by
where r is the radius of a sphere centered at the apex of the cone, A is the area on the sphere subtended by the cone, and Ω is the solid angle.
Solid angle is given the units of
The differential element of solid angle can be determined by considering a small area on the surface of a sphere subtending angles dθ and dφ in spherical coordinates.
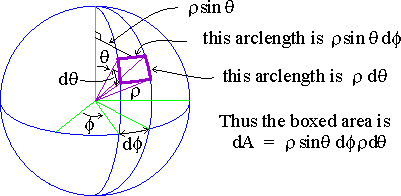
For a sphere of radius ρ the small area has sides of length ρ dθ and $rho; sinθ d&phi. In the limit of infinitesimal angles, the region is a square of area A = ρ² sinθ θ dφ. The element of solid angle is then
The second form is often useful, as seen in the example of the next section.
In the definition of the scattering cross section, we counted any scattering. It is possible to be more specific, and ask how many scattering occur in a particular direction.

The differential cross section for scattering neutrons off a heavy nucleus might have the form dσ/dΩ = σ0(1 + 3cosθ + 3cos²θ) where σ0 is a constant. Describe tha angular distribution and find the total cross section.
Notice that the differential cross section is independent of the azimuthal angle φ. This is quite common -- one usually needs to go to some effort to break azimuthal symmetry, for instance by aligning spins in a magnetic field. To plot this function, look at a few special angles. At θ = 0, dσ/dΩ = 7σ0. At θ = π, dσ/dΩ = σ0. At θ = π/2, dσ/dΩ = σ0. And find any minima and maxima from the zeroes of the derivative, d²σ/dΩdθ = -3σ0sinθ(1 + 2cosθ). This has zeroes at θ = 0 and π, and when cosθ = -1/2, or θ = 2π/3. The first two are maxima, and the third is a minimum. We already have the value of the function at the maxima, when cosθ = -1/2 we find dσ/dΩ = σ0/4. Note that the minimum is positive, as it must be. From this information we can sketch the cross section as a function of θ
To find the total cross section, we integrate the differential cross section the full solid angle, that is over 0 < θ < π and 0 < φ < 2π. The integral is a little easier to do use the d(cosθ) trick. Notice that the minus sign is canceled by reversing the limits of the integral.
![]()