In Taylor, read sections 15.11 -- 15.14 for today and 15.15 -- 15.17 for Wednesday.
The light cone is a helpful way to visualize aspects of realtivity. The light cone is typically drawn in two spatial dimensions and the time dimension.
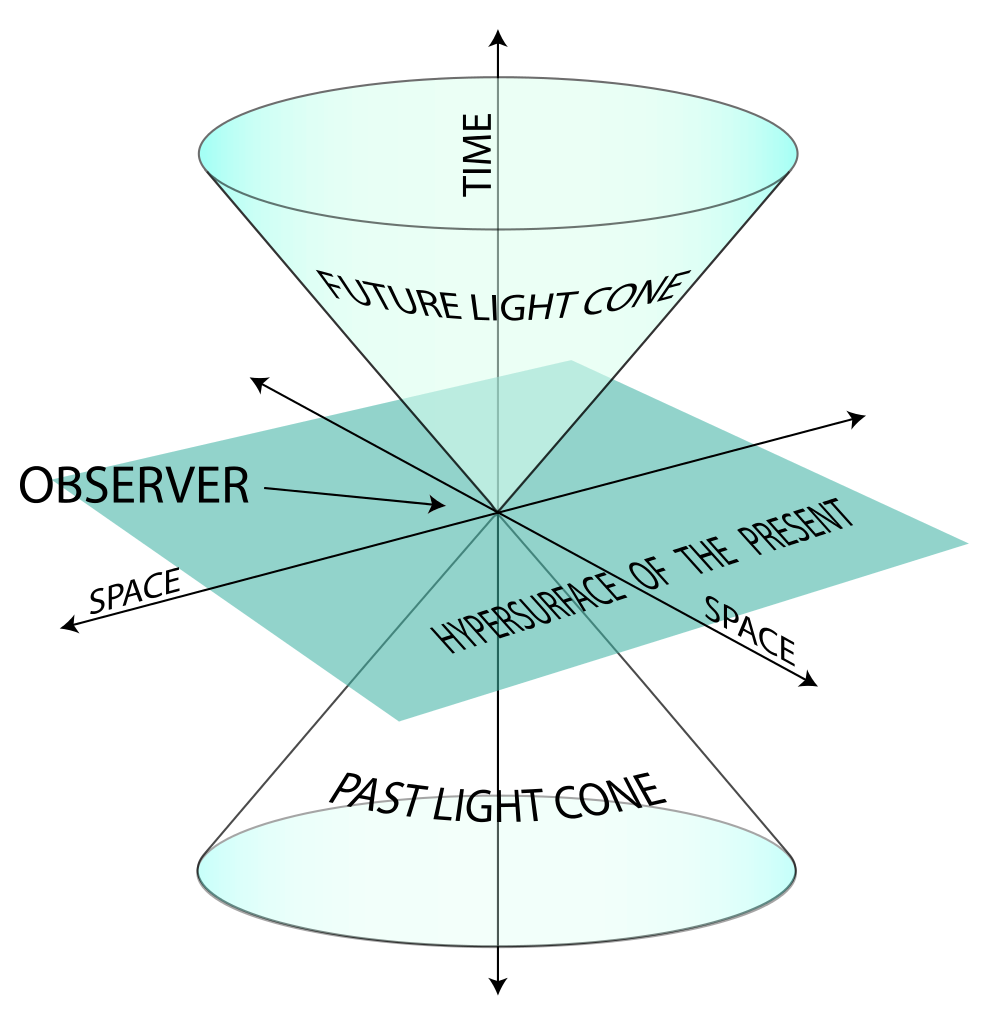
The light cone is drawn so that it traces out the points satisfying x⋅x = r² - c²t² = 0. The light cone has six distinct regions:
The origin at x=0, t=0 represents now, the present time at the present location. All other events are then located relative to now in a particular frame of reference.
Consisting of all the points that can be reached by light propogating outward from now. That is, if we flash a light at the instant of now, the light, traveling in vacuum, could reach the points lying on the cone with t>0.
Consisting of all the points from which light could propogate to now now. That is, if light was flashed at a time t<0 and place lying on the backward light cone, the light, traveling in vacuum, could reach now.
The points inside the forward light cone. Events at these points can be influenced from now.
The points inside the backward light cone. Events at these points can have an influence on now.
The points outside the light cone can have no influence on now and cannot be influenced by now. There is also the odd result that any of these points can be transformed to a frame where their time is earlier, the same as, or later than now. That is, time ordering has no meaning outside the light cone.
Another 4-vector is the wave four-vector k = (k, ω/c). We know it is a four-vector because the equation for a sinusoidal plane wave is
where δ is an arbitrary phase that we can ignore for this discussion, k is the wave vector and ω is the frequency. For light, ω = c|k| The phase of the wave is given k⋅x = k⋅x - ωt, and the phase will be the same for all observers. Therefore k must be a four-vector.
In another frame, the wave four-vector is Lorentz transformed like any other four-vector. Assume we apply a boost in the 1 direction. For light is propagating at an angle θ to the 1-direction, k1 = (ω/c) cosθ. The frequency in the moving frame is the fourth component of the tranformed k four-vector, multiplied by c
The usual way to write this is to take ω' = ω0 as the frequency of light in the rest frame of the source, and ω as the frequency in the observer's frame for a source moving with velocity V at angle θ relative to the observer. Then

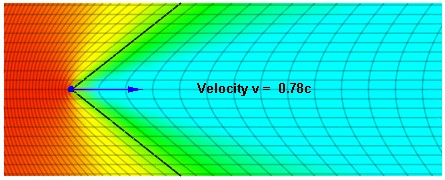
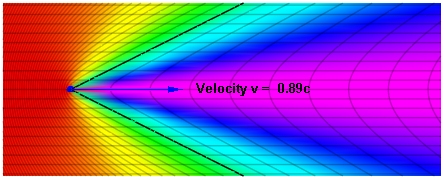
Note that there is a Doppler shift even when the source is moving perpendicular to the observer, θ = ±π/2. When cosθ = 0, the Doppler shift is
Massless particles don't make sense in classical mechanics; a massless particle has zero kinetic energy and zero momentum, and may just as well be ignored. At first glance, relativity also seems to have no room for massless particles since p = γβmc and E = γmc².
But on closer inspection, it is seen that they can exist, with finite momentum and energy. This is possible by treating the above equations in the limit that m → 0, and simultaneously v → c meaning that β → 1 and γ → ∞. In this limit E = pc. This definition also agrees with the definition of photon energy by Planck and Einstein, E = hν = (h/2π) ω.
Collisions are one of the most important applications of special relativity. The study of subatomic objects (electrons, nuclei, protons, neutrons, quarks, ...) is only possible by probing one object with another through collisions, and the energies involved mean that the colliding particles are normally relativisitic.
Collisions are commonly discussed in one of two frames, the lab frame and the CM frame. The lab frame is whatever frame the experiment is carried out in, physically. The CM frame, as we found in earlier chapters, is useful since the total momentum of the system is zero. This still holds in relativistic problems, only now we use the relativistic four-momentum and find the frame where the sum of the spatial components (p1, p2, and p3) are zero
One particular advantage to this frame is in two particle scattering, the final 3-momenta of the two emerging particles are equal in magnitude and opposite in sign. This is a nice simplification to the overall problem.
The lab frame normally represents the frame of reference in which a measurement apparatus is at rest, and is therefore the frame in which the scattered particles are measured. An example of this is the Rutherford scattering experiment, where an incoming beam of alpha particles strikes a target foil, at rest in the lab frame, and the outgoing alpha particles are observed in an apparatus, also at rest in the lab frame. The scattering angle is measured in the lab frame. In the text, the target nucleus is assumed to be much, much heavier than the alpha particle, so that the lab and CM frames are essentially equal, but for light nuclei (aluminum for instance) this is not exactly true and the scattering angle should be transformed to the CM frame for comparison with the theoretical expression.
High energy collisions of two photons can yield electron-positrons pairs. Due to the cosmic microwave background radiation (black body spectrum with T = 2.725K), this process sets an upper limit to the energy of photons that can freely propagate across galactic distances. Find the threshold energy (in eV) for photons to scatter (inelastically) into an electron-positron pair in the CM frame. Determine the threshold energy for a photon to scatter with a micrwave background photon (peak energy of the spectrum) and produce an electron-positron pair (this is the lab frame).
A positron is the anti-particle of an electron; it has the same mass (mec² = 511keV) but opposite charge. The energy of the scattered particles (electron and positron) is the sum of their rest energies plus kinetic energies, Ef = 2mec² + Te + Tp. The threshold energy is the smallest possible energy for the process to proceed, and this occurs when the kinetic energies are zero, Ef = 2mec². The photon is a massless particle, so it's four-vector is p = (p3, p3), where p3 is the 3-momentum. In the CM frame, the two photons have equal and opposite 3-momenta, so their total energy (fourth component) is 2p3c. Setting this equal to the threshold energy yields the photon energy of Eγ = p3c = mec².
The energy of a photon at the peak of a blackbody spectrum is Eμ = hc/λmax = 2π(hbar)cT/b = 2π(197.3×10-9 eV m)(2.725 K)/(2.898×10-3 m K) = 1.165×10-3eV. To determine the threshold energy for a colliding photon to produce an electron-positron pair, note that in the CM, the sum of the photon four-momenta is P = (0, 0, 0, 2mec;), and its square is an invariant, P² = -4(mec)². For scattering off microwave photons, P = pγ + pμ = (pγ - pμ, 0, 0, pγ + pμ), and equating the squares, we find (pγ - pμ)² - (pγ + pμ)² = -4pγpμ = -4(mec)². Therefore the threshold energy of the photon is Eth = pγc = me²c4 / Eμ = (5.11×105 eV)² / (1.165×10-3eV) = 2.24×1014eV.
![]()