Read 16.1, 16.2, and 16.4 for Today. Read 16.5 -- 16.6 for Monday.
Review the derivation of the Euler--Lagrange equation from Chapter 6.
Most of this course has dealt with the motion of point particles, with an excursion into rigid body motion in Chapter 10. Continuum mechanics deals with the behavior of systems composed of a large, essentially infinite, number of particles, where the relative positions of the particles are not fixed.
In continuum mechanics we treat the properties of a material, principally density, as being a continuous function, despite knowing that at the atomic scale this is no longer true. Despite the fact that solids, liquids, and gases are not continuous at the atomic scale, treating them as if they are produces results in agreement with experiment. This could be expected since most systems that we deal with are sufficiently large that volume elements can be defined that are small on the scale of the system and large on atomic scales. For instance, a volume that is 1mm³ is a small part of an airplane wing or building beam, yet can contain on the order of 1020 atoms.
The first system we will consider is a string. We will derive the equation for a wave on the string --- a wave equation. Taylor does this using Newton's laws. Here I derive it using the Lagrangian, following material from Marion & Thornton (up to taking the continuous limit of an infinite number of masses, then from Kibble & Berkshire for the discussion of the generalization of the Euler-Lagrange equation.
A taut string of length L can be approximated by n masses m connected by small strings of length dl, in the limit that n → ∞ and dl → 0 such that (n+1) dl → L and n m → M, the total mass of the string. The situation is pictured below.
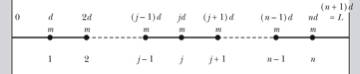
We will say that the string (or all the connecting strings in the picture above) is under tension τ. We allow each of the masses to move in a plane perpendicular to the string, the transverse direction. Call the displacement of the ith mass qi, and its velocity qidot. We are assuming that the displacements are small, so that only the perpendicular coordinate changes, and the motion of each mass is perpendicular to the equilibrium position of the string. This approximation also allows us to treat the tension as constant and uniform along the string.
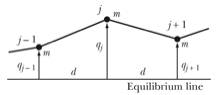
The potential energy is the just the work done to stretch each element of the string at constant tension, Uj = τ Δ lj where τ is used for the tension in the string to avoid confusion with the kinetic energy T, and
Sum up the potential for all the elements
We take the sum from 1 to n+1, where the positions q0 and qn+1 are the positions of the ends of the string, both zero by definition.
The kinetic energy is given the sum of the kinetic energies for each mass
The sum can be safely taken from j=1 to n+1, where qn+1dot = 0 since it is a fixed point. Then both sums have the same range and we can write the Lagrangian
It is possible to explore the results obtained with this discrete model, but let us pass to the limit of n → ∞. Let us parameterize the string horizontally by the coordinate x, and define the position of the string at a particular instant and coordinate as u(x, t). In this case, m → μ dx where μ is the mass per unit length, M/L for the string, qjdot = ∂u(x, t)/∂t, (qj-1 - qj) → ∂u/∂x dl, and the sums over j become integrals over dx. The Lagrangian becomes
where we use udot for the partial derivative with respect to time and u' for the partial derivative with respect to distance x. The piece inside the integral is called the Lagrangian density. Its integral is the Lagrangian. If action is the integral of the Lagrangian from time t0 to t1
As done in the calculus of variations, the idea is that the actual motion is the one that results in a minimum of the action for given initial conditions. The action is of the form
Note that it is standard to use L for a Lagrangian density and L for a Lagrangian. Pay attention to this change in the following discussion.
To minimize the action we want δS = 0. In terms of the integral of the Lagrangian density this becomes
We follow the same steps as in the derivation of the Euler-Lagrange equations in Chapter 6, that is, integrate the second and third terms by parts, and use the requirement that the deviations are zero at the endpoints of the motion. Start with the change δu' = ∂( δu )/∂x then
and likewise for the time derivative term. The result is
and since δu is arbitrary, the only way that this is zero is if the quantity in square brackets is zero
This is the generalization of the Euler-Lagrange equation. In the case of the taut string
This depends on just udot and u', not u. Applying the generalized Euler-Lagrange yields
which simplifies to the one-dimensional wave equation
The constant c = √(τ/μ) will be shown to be the wave speed on the string, and depends on the tension in the string τ and the mass density μ.
The wave equation is a second order partial differential equation.
The initial conditions can be considered as the position and velocity of each element of the string at t=0, u(x, 0) and udot(x, 0).
For the taut finite string, we also require that the ends remain fixed for all times, u(0, t) = u(L, t) = 0.
The general solution consists of two independent functions. These are most easily envisioned as a wave moving to the right f(x-ct), and a wave moving to the left g(x+ct)
The conditions for the ends of a fixed string yield the relations
or g(x) = -f(-x) and then
Substitute x = L-ct and then it is easy to see that this condition implies that f is 2L periodic, f(x) = f(x-2L). The general solution is then
with f periodic. The initial conditions at t=0 yield
The odd part of f is given by the initial position while the even part comes from the initial velocities.
For systems with other end conditions (semi-infinite string with one end fixed, semi-infinite string with one end free to displace, a beam supported at points not at the ends, and so forth), the resulting general solution will have slightly different requirements, but we still start from the waves moving in opposite directions.
While this has been derived for a taut string, the results can be generalized to other systems that act one--dimensional. An important example is a beam, from the steel I--beams used in construction to the cantileter that supports the tip of an atomic force microscope (AFM). We have an AFM in the advanced lab (PHY6850). Measurements of the thermal noise in the cantilever--tip system can be Fourier transformed to find the natural frequency (fundamental frequency) of the system.
We can generalize the wave equation to more dimensions in a straight--forward way. Add a y coordinate and allow displacements in the z direction to get the wave equation for a membrane. Define the displacement to be a pressure, and expand to three dimensions to have the wave equation for a fluid (or a gas, but a gas is considered a fluid for these purposes).
It is normal to make use of the ∇ operator to write the wave equation in a more compact form
The ∇² operator is called the Laplacian. It appears in many places in quantum mechanics and E&M. In all of these cases, the three dimensional wave equation supports many types of waves. Of special significance are plane waves and spherical waves.
![]()