Read 16.5 -- 16.6 for Today. Read 16.7 for Wednesday.
The next goal in studying continuous, 3-dimensional media is to devise some equations of motion for systems, the equivalent of Newton's second law. The equation of motion for a solid and a liquid (includes gases) differ, largely due to shear forces. A shear force is a force tangential to the face of an object (or imaginary volume element), as opposed to a force of compression or tension that is perpendicular to the face.
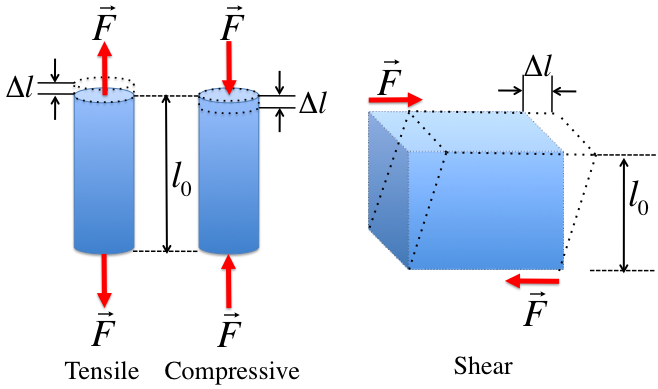
In fact, a basic definition of a liquid (at rest) is that it does not support shear forces.
For finding an equation of motion, the medium is subdivided into infinitesimal volume elements. The shape of a volume element is arbitrary; it should be chosen to best meet the needs of a particular problem. A typical volume element is a 3-dimensional rectangular volume, but we will soon make use of a prism shape.
The volume element divides space into interior (inside) and exterior (outside). Surface areas are represented by outward--pointing normal vectors of length proportional to the area.
There are two types of forces on a volume element: volume and surface forces.
Volume forces are proportional to the volume of the element. Examples of volume forces are gravity, proportional to the mass in the volume ρ dV, and electrostatic forces proportional to the charge in the volume ρq dV.
Surface forces are proportional to the surface area on which it acts. Tensile, compressive, and shear forces are surface forces.
When there are no shear forces, or the shear is very small as in a low viscosity fluid, the pressure in a medium is isotropic, that is, the same in all directions. This is the usual way you have seen pressure used in physics courses. The proof of this statement relies on the different scalings of volume and surface forces --- a relation that contains both can only be satisfied if each set satisfies a relation separately.
Consider two rectangular surface elements dA1 and dA2, that touch along one edge, and are the same length in the direction of that common edge and along the perpendicular edge so that they are the same area. Add 3 more surfaces to create a prism, with surface elements dA3, dA4, and dA5. Let surfaces 4 and 5 be the ends of the prism and 3 be the base.
Due to internal pressure, each surface experiences an outward force Fi = pi ni dAi
. We allow that there can also be volume forces, for instance, gravity. The total force isor if we group all the surface forces on the left and volume forces on the right
This relation must hold if we scale up or down the size of the prism. Since surfaces and volume scale differently, the only way this relation holds is if each side is separately zero. Therefore
The end forces F4 and F5 point in a plane perpendicular to the other 3 forces. They can be ignored for the rest of this demonstration.
Sides 1, 2, and 3 form an isosceles triangle. The forces F1 and F2 must be equal in magnitude so that their sum will cancel with F3. If they have equal areas and equal magnitudes, then p1 = p2. Since the directions of the surfaces are arbitrary, this implies that the pressure must be the same in all directions, that is, the pressure is isotropic.
There are at least three ways a stress can appear:
Stress always has the dimensions of force/area.
The result of stress is often a deformation or a strain. Some examples of strain are
The relation between stress and strain is characterized by the elastic modulus. Again, there are several examples:
To summarize
![]()