Recall from last lecture:

Rules for Drawing Feynman Diagrams (version one)

1. The horizontal direction is the horizontal direction, increasing from left to right. The vertical direction represents all other spatial directions. The left side of the diagram represents the initial state, and the right side represents the final state. (Again, some authors draw time in the vertical direction, in which case you can rotate the drawing clockwise by 90° to get our convention.)
2. Fermions are drawn as continuous, solid lines. A fermion line can end only in the initial or final states (left or right side of the diagram).
3. Bosons are drawn as dashed lines, wavy lines, or loopy (helix or spring-like) lines. Photons are represented by wavy lines, gluons by loopy lines, and Z° or W^± by either wavy lines or dashed lines.
4. Lines should be labeled to avoid confusion.

This is enough to start with, let's use these to look at a more complex interaction.

The Basic QED Interaction Vertex

In Quantum Electrodynamics (QED) the basic interaction vertex is the junction of two fermion lines with a photon. The two fermion lines are part of a single, unbroken line. We draw an arrow on the lines to indicate the time sense of the fermion. An arrow pointing forward in time identifies that line as a particle. An arrow pointing backward in time identifies that line as an antiparticle.

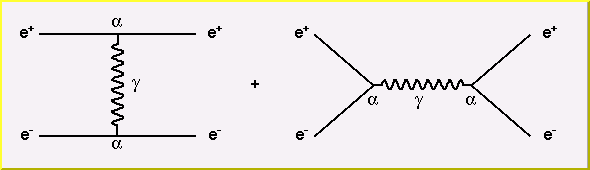
Many complex processes can be built from this basic QED vertex. Let's look at some examples, beginning with Bhabha scattering.

Bhabha Scattering

Bhabha scattering is named for the Indian physicist who first calculated the process.

Pair Annihilation, Pair Production, and Compton Scattering

A valid Feynman diagram can be reflected and twisted to produce other valid Feynman diagrams. An example of this process is given by the three basic diagrams for the processes of pair annihilation, pair production, and Compton scattering. Notice that in these processes, the exchanged particle is an electron (fermion) not a photon (boson).

Virtual Particles

Any particle in a Feynman diagram that is not part of the initial or final state is called a virtual particle. It is standard convention to impose energy and momentum conservation at each vertex. However, in doing so we must give up something. What we give up is the "mass constraint" on virtual particles. Virtual particles can have a mass that is different from the mass of their real counterparts. This can be readily seen by considering the diagram for a single photon producing an e⁺e^- pair. This process cannot occur in vacuum for a real massless photon, and conserve energy and momentum simultaneously, as you will demonstrate in a homework problem.

Giving up the defined mass is justified by Heisenberg's uncertainty relation, DE Dt > hbar/2. Since virtual particles exist for only a finite time, their energy is uncertain, and the mass is part of the energy of the particle. We say that virtual particles are "off the mass shell" while real particles are "on the mass shell".

Higher Order Diagrams

The Feynman diagrams we have looked at thus far are known as "tree" diagrams. They represent the most basic interaction that transforms the initial state into the final state, and therefore normally involve the exchange of only one photon or one fermion. They also represent the lowest order diagram in a series of diagrams with successively more particles exchanged. As each diagram represents the integral for a matrix element, the series of diagrams corresponds to a series of integrals that must be summed to get the entire matrix element. If higher order diagrams (integrals) are sufficiently smaller than lower order diagrams, then the series is perturbative.

Jargon and Lingo