Recall from last lecture:
Quantum Electrodynamics (QED): the basic interaction vertex
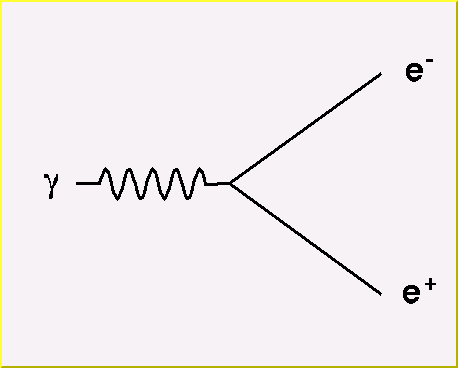
Quantum Chromodynamics (QCD): the basic interaction vertex

The Weak Force
The weak force is mediated by the massive, spin=1 bosons W+, W-, and Z°, known collectively as the intermediate vector bosons.
The weak interactions are classified as charged, those mediated by the W bosons, and neutral, those mediated by the Z boson.
Historically the charged interactions were known well before the neutral.
The charged interaction is responsible for beta decay of nuclei.
The neutral interaction was predicted by the electroweak theory of Weinberg, Glashow, and Salam, and was undeniably confirmed by the subsequent discovery of the Z° with precisely the properties predicted by their theory.
For reasons that will become clear later, weak interactions continue to play an important role in particle physics research.
The electromagnetic force couples to electric charge; the strong force couples to color (strong charge).
There is no term for what the weak force couples to, but we may use the term weak charge in obvious analogy.
All of the particles (quarks and leptons) carry weak charge.
Since neutrinos don't have electric charge or color, they only experience the weak force and gravity.
The weak force is the only force that couples between quark flavors (types) making it important in the study of quark decays.
The weak force doesn't couple between leptons and quarks, so our discussion will focus first on weak interactions involving leptons, then quarks, and, for completeness, I'll discuss some diagrams required for internal consistency of the electroweak theory.
Leptons
 The fundamental charged vertex couples a W with a charged lepton and the corresponding neutrino.
Conservation of lepton number is guaranteed because the W couples only to leptons of the same generation (first generation = electron type, second generation = muon type, and third generation = tau type).
The fundamental charged vertex couples a W with a charged lepton and the corresponding neutrino.
Conservation of lepton number is guaranteed because the W couples only to leptons of the same generation (first generation = electron type, second generation = muon type, and third generation = tau type).
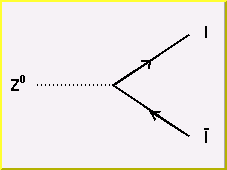 The fundamental neutral vertex couples a Z° with two lepton lines.
The fundamental neutral vertex couples a Z° with two lepton lines.
Quarks
The couplings to quarks differ in a subtle way.
Recall that we don't have a conservation law for quark generation as we do for lepton number (generation).
To aid in the following discussion, I'll introduce the following notation:
- Qi represents any one of the 6 quark flavors.
I have already used this notation in diagrams where the vertex conserves quark flavor, like the gluon and photon vertices.
- Ui represents any one of the 3 up-type quarks, u, c, or t.
- Di represents any one of the 3 down-type quarks, d, s, or b.
With this notation, let's look at the charged and neutral current interactions.
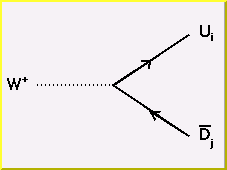 The fundamental charged vertex couples a W with an up type quark and a down type quark.
The fundamental charged vertex couples a W with an up type quark and a down type quark.
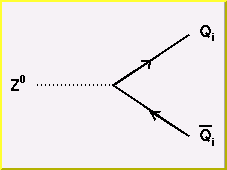 The fundamental neutral vertex couples a Z° with two quark lines.
The fundamental neutral vertex couples a Z° with two quark lines.
Copyright © Robert Harr 2003
 The fundamental charged vertex couples a W with a charged lepton and the corresponding neutrino.
Conservation of lepton number is guaranteed because the W couples only to leptons of the same generation (first generation = electron type, second generation = muon type, and third generation = tau type).
The fundamental charged vertex couples a W with a charged lepton and the corresponding neutrino.
Conservation of lepton number is guaranteed because the W couples only to leptons of the same generation (first generation = electron type, second generation = muon type, and third generation = tau type).


 The fundamental neutral vertex couples a Z° with two lepton lines.
The fundamental neutral vertex couples a Z° with two lepton lines.
 The fundamental charged vertex couples a W with an up type quark and a down type quark.
The fundamental charged vertex couples a W with an up type quark and a down type quark.
 The fundamental neutral vertex couples a Z° with two quark lines.
The fundamental neutral vertex couples a Z° with two quark lines.