Lecture 15

Recall from last lecture:

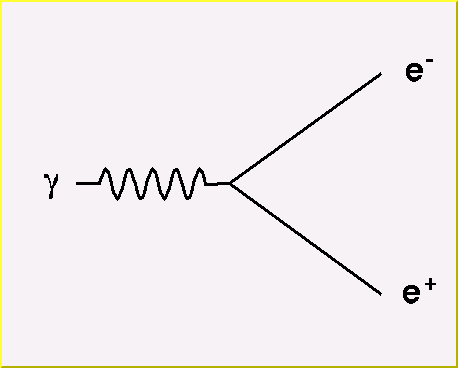
Quantum Electrodynamics (QED): the basic interaction vertex

Quantum Chromodynamics (QCD): the basic interaction vertex

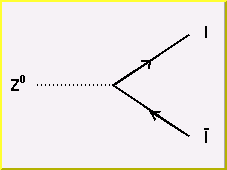
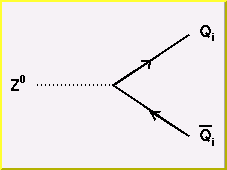
The Weak Force: the basic interaction vertices

Wlnu vertex Zll vertex

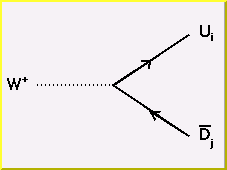
WUD vertex ZQQ vertex

The fundamental charged vertex couples a W with an up-type quark and a down-type quark. The up-type and down-type quarks can come from different generations, i.e. u with s, d with c, or c with b. The allowed amount of cross-generational coupling is determined by the Cabibo-Kobayashi-Maskawa (CKM) matrix.

The picture is that the quarks that form hadrons are mass eigenstates, while what couples to the W and Z are the weak eigenstates, and for the quarks the two are not lined up. By convention we choose our phase such that the up-type quarks have no mixing between mass eigenstates and weak eigenstates. Then the weak eigenstates of the down-type quarks are linear combinations of the mass eigenstates given by:

d'	=	V_ud	V_us	V_ub	d
s'		V_cd	V_cs	V_cb	s
b'		V_td	V_ts	V_tb	b

With the U/D notation defined above, we can write this as

D'_i = S_jV_ijD_j

The nine elements of the CKM matrix are complex numbers -- therefore 18 separate real numbers are needed to specify the matrix. However, the matrix is unitary, meaning that

VV^* = V^*V = 1

This relation yields 12 independent equations among the 18 numbers, and additionally we are free to choose two arbitrary phases. We are left with just 4 numbers that describe this matrix.

Electroweak

WWgamma and WWZ vertices Some additional diagrams are needed to complete the electroweak theory. The two most important are the WW