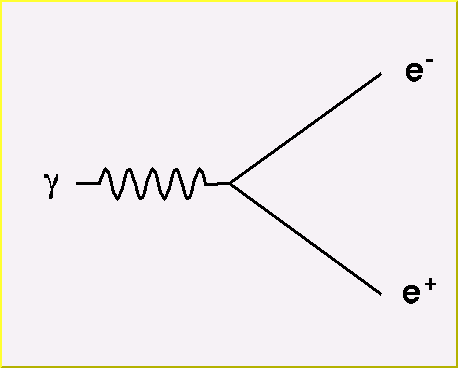
Quantum Electrodynamics (QED): the basic interaction vertex
Quantum Chromodynamics (QCD): the basic interaction vertex

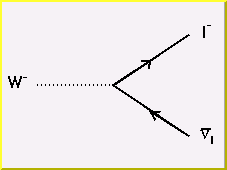
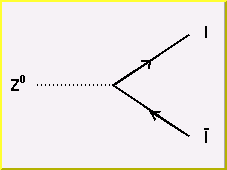
The Weak Force: the basic interaction vertices


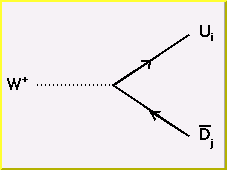
The fundamental charged vertex couples a W with an up-type quark and a down-type quark. The up-type and down-type quarks can come from different generations, i.e. u with s, d with c, or c with b. The allowed amount of cross-generational coupling is determined by the Cabibo-Kobayashi-Maskawa (CKM) matrix.
The picture is that the quarks that form hadrons are mass eigenstates, while what couples to the W and Z are the weak eigenstates, and for the quarks the two are not aligned. By convention we choose our phase such that the up-type quarks have no mixing between mass eigenstates and weak eigenstates. Then the weak eigenstates of the down-type quarks are linear combinations of the mass eigenstates given by:
| d' | = | Vud | Vus | Vub | d |
| s' | Vcd | Vcs | Vcb | s | |
| b' | Vtd | Vts | Vtb | b |
Two common parameterizations of the CKM matrix are used. The first is exact, but does leave one with a certain numbness from staring at it; the second is an approximation that parameterizes each of the 9 terms as a power series in parameters of varying size, highlighting the structure of the magnitues of the terms.
The first parameterization is in terms of 3 real angles, θ12, θ23, and θ13, and a complex phase angle δ13. The subscripts on the angles serve to remind us of where the angles have their primary effect: for example, 12 means the angle parameterizes the mixing between the first and second generation quarks, d and s. If a particular angle vanishes, so does the mixing between the corresponding generations. We use a shorthand for the cosine and sine of these angles: cij = cos θij, and sij = sine θij. Then the CKM matrix can be written:
| V = | c12c13 | s12c13 | s13e-iδ13 |
| -s12c23-c12s23s13eiδ13 | c12c23-s12s23s13eiδ13 | s23c13 | |
| s12s23-c12c23s13eiδ13 | -c12s23-s12c23s13eiδ13 | c23c13 |
The second common parameterization was first written down by Lincoln Wolfenstein and is commonly known as the Wolfenstein parameterization. It highlights the relative sizes of the terms by expanding them in a power series in λ~=s12.
| |V| = | 1 - λ2/2 | λ | A λ3(ρ-iη) |
| -λ | 1 - λ2/2 | A λ2 | |
| A λ3(1-ρ-iη) | -A λ2 | 1 |
From present measurements we can estimate the magnitudes of the elements of the CKM matrix. They are approximately:
| |Vij| = | 0.975 | 0.22 | 0.003 |
| 0.22 | 0.974 | 0.04 | |
| 0.09 | 0.04 | 0.999 |
At a W-vertex with up-type-quark i and down-type-quark j, the coupling is proportional to Vij. This allows us to estimate the relative rates of otherwise similar processes