Lecture 16

Recall from last lecture:

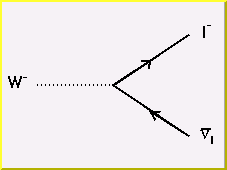
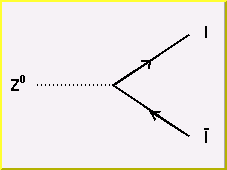
The Weak Force: the basic interaction vertices

Wlnu vertex Zll vertex

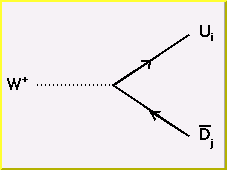
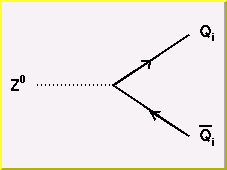
WUD vertex ZQQ vertex

The W vertex receives an term corresponding to the quark flavors at the vertex. These terms are conveniently arranged in a 3x3 matrix called the Cabibbo-Kobayashi-Maskawa (CKM) matrix:

V_CKM =	V_ud	V_us	V_ub
	V_cd	V_cs	V_cb
	V_td	V_ts	V_tb

The CKM matrix is unitary:

VV^† = V^†V = 1

Just 4 numbers that describe this matrix.

The Z Vertex

A Z boson couples only to quarks of the same weak eigenstate. Due to the unitarity property of the CKM matrix, this results in couplings between quarks of the same mass eigenstate.

Flavor quantum numbers

The strong, electromagnetic, and neutral weak particles couple between quarks of the same flavor (type). The only way to change quark flavor is through charged weak processes. This leads to the idea of flavor quantum numbers to describe the quark content of hadrons. (This also is due to the mass differences between the strange, charm, and bottom quarks. The smallness of the up and down quark masses relative to the hadron masses allows quantum mechanical mixing between states such as u anti-u and d anti-d. For this reason, we don't use quantum numbers for up and down, but use something called isospin to be introduced later.) The first quantum number is S for strangeness. It was intorduced to help explain the fact that strange particles are readily produced in pairs in high energy collisions, but live relatively long times. That is, they are produced via strangeness-conserving strong or electromagnetic interactions, but decay individually in strangeness-changing weak decay. Basically a hadron containing a strange quark has strangeness -1, and a particle with an anit-strange quark has strangeness +1. (To help remember this, note that the flavor quantum numbers have the same sign as the charge of the corresponding quark.) Likewise a hadron containing a charm quark has charmness +1, and a hadron containing a bottom quark has bottomness -1 (top quarks decay to rapidly to form hadrons).

Hadrons are now described by the following quantum numbers:

Q: charge
B: baryon number (=+1 for baryons, -1 for anti-baryons, 0 for mesons)
S: strangeness
C: charmness
~B: bottomness

If any of the last 3 are violated, then the charged weak interaction is involved. These quantum numbers are often enough to deduce the quark content of a hadron. First, from the baryon number, determine if 3 quarks, 3 anti-quarks, or a quark-anti-quark pair are required. Second, allocate strange, charm, and bottom quarks as specified by the quantum numbers. Third, fill in the missing quarks with appropriate mixtures of up, down, anti-up, or anti-down to get the correct charge.

Note that not all combinations of quantum numbers correspond to real hadrons.